(Solved): (20 points) Customers enter a fast-food restaurant according to an exponential interarrival time wi ...

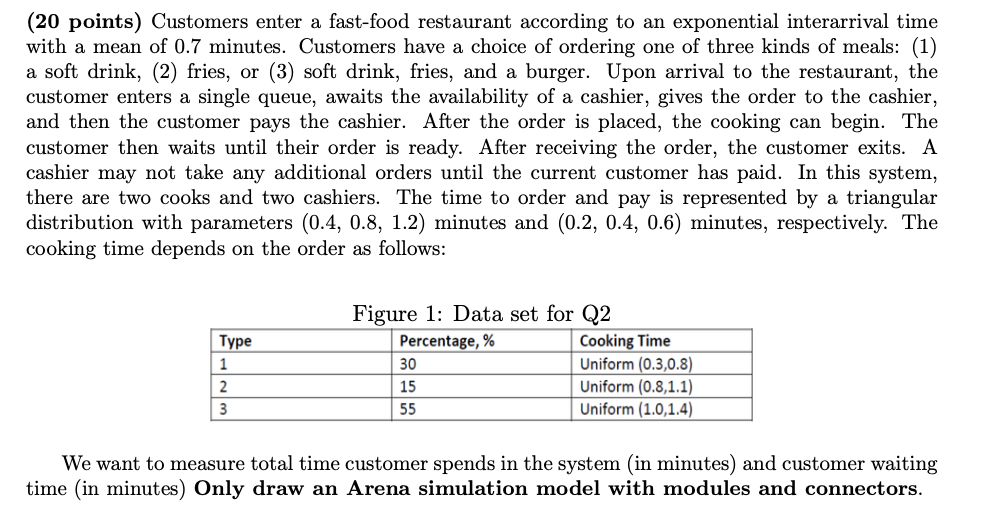
(20 points) Customers enter a fast-food restaurant according to an exponential interarrival time with a mean of 0.7 minutes. Customers have a choice of ordering one of three kinds of meals: (1) a soft drink, (2) fries, or (3) soft drink, fries, and a burger. Upon arrival to the restaurant, the customer enters a single queue, awaits the availability of a cashier, gives the order to the cashier, and then the customer pays the cashier. After the order is placed, the cooking can begin. The customer then waits until their order is ready. After receiving the order, the customer exits. A cashier may not take any additional orders until the current customer has paid. In this system, there are two cooks and two cashiers. The time to order and pay is represented by a triangular distribution with parameters ( \( 0.4,0.8,1.2 \) ) minutes and ( \( 0.2,0.4,0.6 \) ) minutes, respectively. The cooking time depends on the order as follows: We want to measure total time customer spends in the system (in minutes) and customer waiting time (in minutes) Only draw an Arena simulation model with modules and connectors.