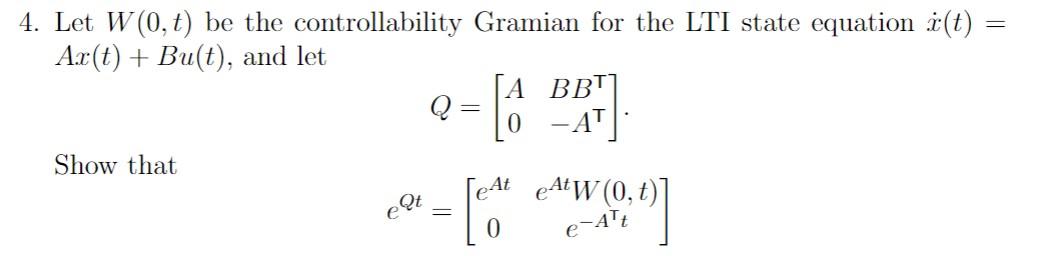(Solved): 4. Let \( W(0, t) \) be the controllability Gramian for the LTI state equation \( \dot{x}(t)= \) \ ...

4. Let \( W(0, t) \) be the controllability Gramian for the LTI state equation \( \dot{x}(t)= \) \( A x(t)+B u(t) \), and let \[ Q=\left[\begin{array}{cc} A & B B^{\top} \\ 0 & -A^{\top} \end{array}\right] . \] Show that \[ e^{Q t}=\left[\begin{array}{cc} e^{A t} & e^{A t} W(0, t) \\ 0 & e^{-A^{\top} t} \end{array}\right] \]