(Solved): Problem 3. Projectile motion. (15 points) From the top of a tower (height \( h \) ), two point mass ...

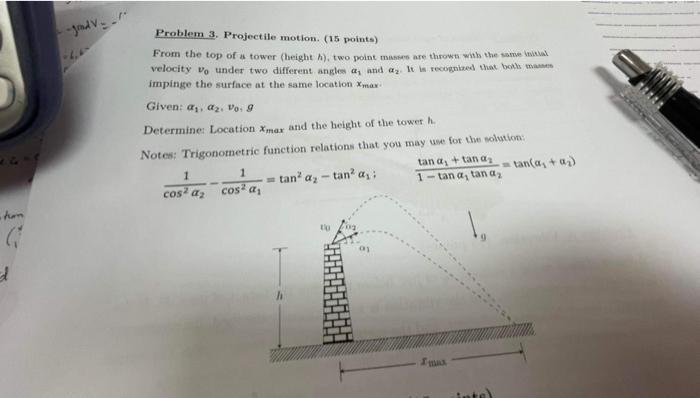
Problem 3. Projectile motion. (15 points) From the top of a tower (height \( h \) ), two point masses are thrown whb the same inutal velocity \( v_{0} \) under two different angles \( \alpha_{1} \) and \( \alpha_{2} \). It is recognized that both masms impinge the surface at the same location \( x_{\max } \). Given: \( \alpha_{1}, \alpha_{2}, v_{0}, g \) Determine: Location \( x_{\max } \) and the beight of the tower \( h \). Notes: Trigonometric function relations that you may use fot the nolution: \[ \frac{1}{\cos ^{2} \alpha_{2}}-\frac{1}{\cos ^{2} \alpha_{1}}=\tan ^{2} \alpha_{2}-\tan ^{2} \alpha_{1} ; \quad \frac{\tan \alpha_{1}+\tan \alpha_{2}}{1-\tan \alpha_{1} \tan \alpha_{2}}=\tan \left(\alpha_{1}+\alpha_{2}\right) \]