Home /
Expert Answers /
Mechanical Engineering /
1-1-polnt-steady-state-temperatures-k-at-three-nodal-points-of-a-long-rectangular-rod-are-as-sho-pa525
(Solved): 1 1 polnt Steady-state temperatures ( K ) at three nodal points of a long rectangular rod are as sho ...
1
1 polnt
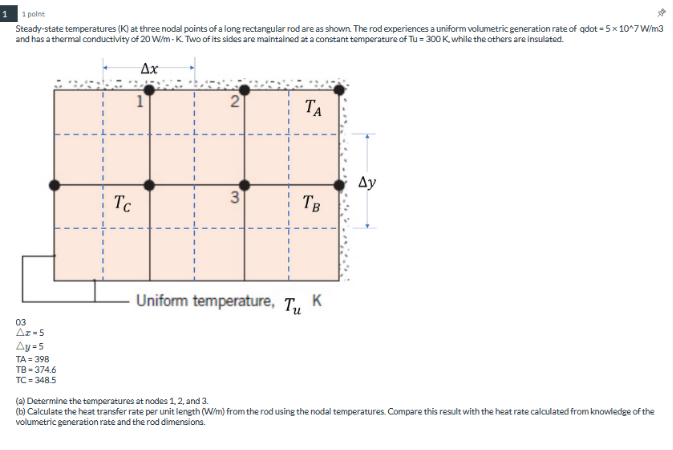
Steady-state temperatures ( K ) at three nodal points of a long rectangular rod are as shown. The rod experiences a uniform volumetric generation rate of qdot =5\times 10^(7)(W)/(m)3 and has a thermal conductivity of 20(W)/(m)*K. Two of its sides are maintained at a constant temperature of Tu=300K, while the others are insulated. The finite difference equation at nodes and C
03
\Delta x=5
\Delta y=5
TA=398
TB=374.6
TC=348.5
(a) Determine the temperatures at nodes 1, 2, and 3.
(b) Calculate the heat transfer rate per unit length ((W)/(m)) from the rod using the nodal temperatures. Compare this result with the heat rate calculated from knowledge of the volumetric generation rate and the rod dimensions.