(Solved): 1. An elevator shown below filled with passengers has a mass of \( 1700.0000 ...

???????

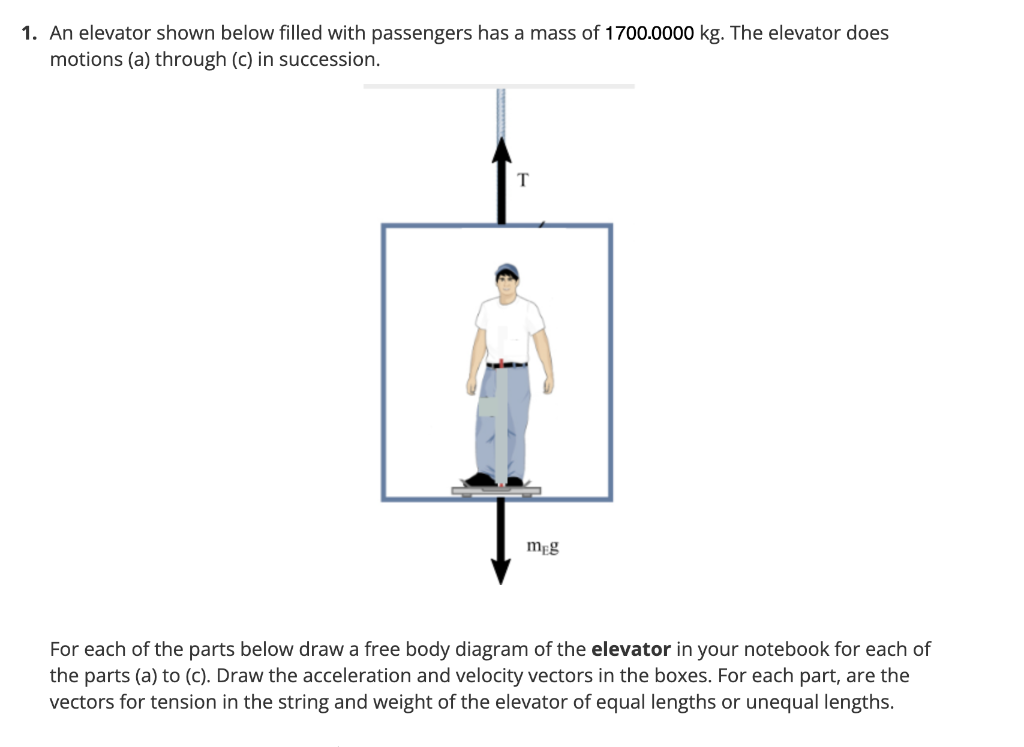
1. An elevator shown below filled with passengers has a mass of \( 1700.0000 \mathrm{~kg} \). The elevator does motions (a) through (c) in succession. For each of the parts below draw a free body diagram of the elevator in your notebook for each of the parts (a) to (c). Draw the acceleration and velocity vectors in the boxes. For each part, are the vectors for tension in the string and weight of the elevator of equal lengths or unequal lengths. 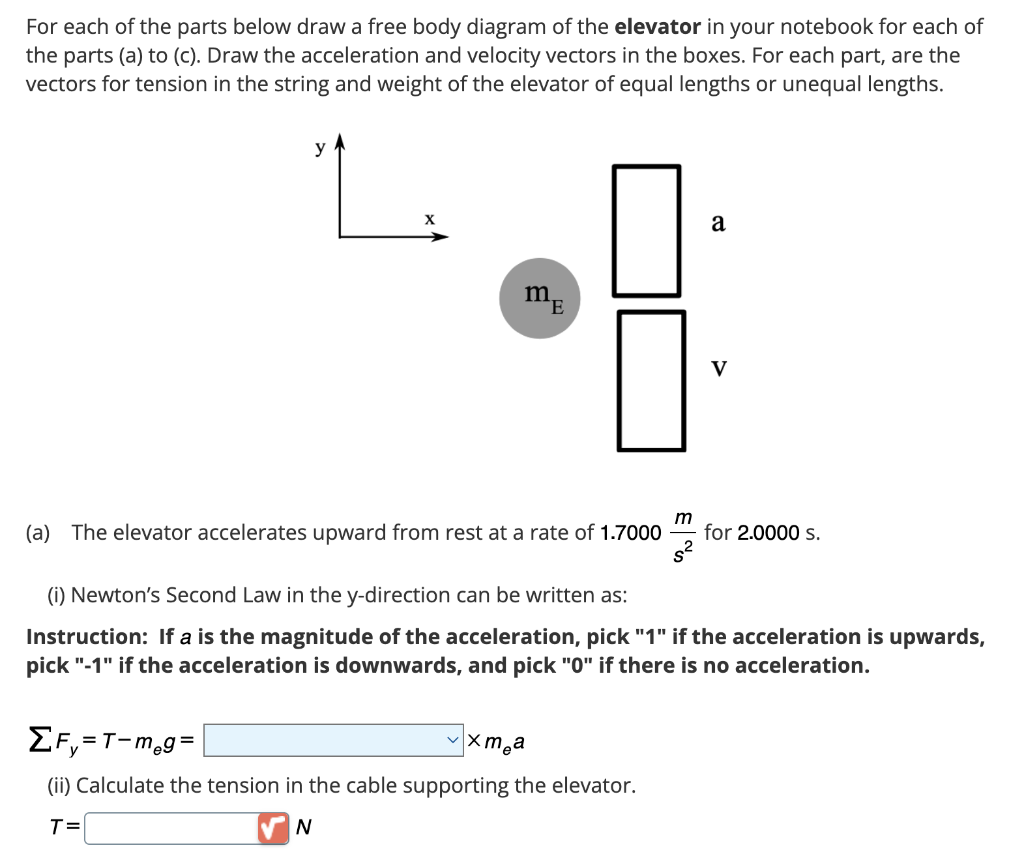For each of the parts below draw a free body diagram of the elevator in your notebook for each of the parts (a) to (c). Draw the acceleration and velocity vectors in the boxes. For each part, are the vectors for tension in the string and weight of the elevator of equal lengths or unequal lengths. (a) The elevator accelerates upward from rest at a rate of \( 1.7000 \frac{\mathrm{m}}{\mathrm{s}^{2}} \) for \( 2.0000 \mathrm{~s} \). (i) Newton's Second Law in the y-direction can be written as: Instruction: If \( a \) is the magnitude of the acceleration, pick "1" if the acceleration is upwards, pick "-1" if the acceleration is downwards, and pick " 0 " if there is no acceleration. \[ \sum F_{y}=T-m_{e} g=\quad \times m_{e} a \] (ii) Calculate the tension in the cable supporting the elevator. \[ T=\quad N \] (iii) How high has the elevator moved during this time? \[ \Delta y=\quad m \] (iv) Calculate the velocity of the elevator after this time. \[ v(t=2.0000 \mathrm{~s})=1 \frac{m}{s} \] (b) The elevator continues upward at constant velocity for \( 8.0000 \mathrm{~s} \). (i) Newton's Law in the y-direction can be written as: Instruction: If \( a \) is the magnitude of the acceleration, pick " 1 " if the acceleration is upwards, pick " \( -1 " \) if the acceleration is downwards, and pick " 0 " if there is no acceleration. \[ \sum F_{y}=T-m_{e} g=1 \quad \times m_{e} a \] (ii) Calculate the tension in the cable supporting the elevator. \( T= \) \[ N \] (iii) How high has the elevator moved during this time? \[ \Delta y=|\quad| m \] (c) The elevator decelerates at a rate of \( 0.8500 \frac{m}{s^{2}} \) for \( 3.2000 \mathrm{~s} \). (i) Newton's Law in the y-direction can be written as: Instruction: If \( a \) is the magnitude of the acceleration, pick "1" if the acceleration is upwards, pick " \( -1 \) " if the acceleration is downwards, and pick " 0 " if there is no acceleration. \[ \sum F_{y}=T-m_{e} g=\mid \quad \times m_{e} a \] (ii) Calculate the tension in the cable supporting the elevator. \( T= \) \( n \) (iii) How high has the elevator moved during this time? \[ \Delta y=1 \quad m \] (d) What is the total distance the elevator has moved up? \[ \Delta y_{n e t}=\quad m \] Reflect: In which case is the tension in the chord pulling the elevator the greatest? Why? Does the tension always equal the weight of the elevator?