(Solved): 1. Identify each of the following basic circular function graphs. x.. (h) (a) 2. Connecting Graphs ...

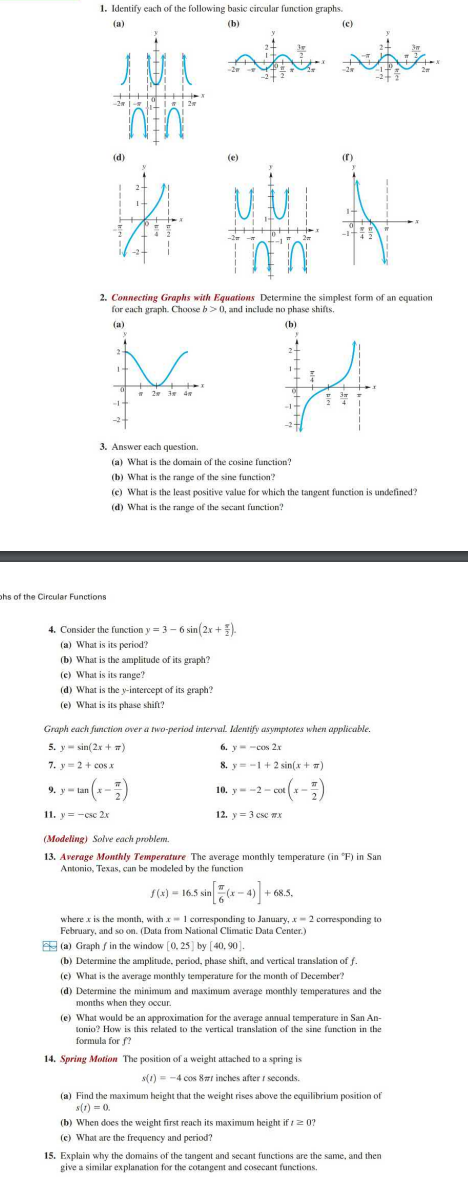
1. Identify each of the following basic circular function graphs. x.. (h) (a) 2. Connecting Graphs with Equations Determine the simplest form of an equation for each graph. Choose $b>0$, and include no phase shifts. 3. Answer each question. (a) What is the domain of the cosine function? (b) What is the range of the sine function? (c) What is the least positive value for which the tangent function is undetined? (d) What is the range of the secant function? Circular Functions 4. Consider the function $y=3?6\sin \left(2x+\frac{?}{2}\right)$. (a) What is its period? (b) What is the amplitude of its graph? (c) What is its range? (d) What is the $y$-intercept of its graph? (e) What is its phase shift? Graph each function over a fwo-period intenval. ldentify asymptoses when applicable. 5. $y=\sin (2x+?)$ 6. $y=?\cos 2x$ 7. $y=2+\cos x$ 8. $y=?1+2\sin (x+?)$ 9. $y=\tan \left(x?\frac{?}{2}\right)$ 10. $y=?2?\cot \left(x?\frac{?}{2}\right)$ 11. $y=?\csc 2x$ 12. $y=3\csc ?x$ (Modeling) Solve each problem. 13. Average Monthly Temperature The average monthly temperature (in ${}^{?}\mathrm{F}$ ) in San Antonio, Texas, can be modeled by the function $f(x)=16.5\sin \left[\frac{?}{6}(x?4)\right]+68.5,$ where $x$ is the month, with $x=1$ corresponding to January, $x=2$ corresponding to February, and so on. (Data from National Climatic Data Center.) $\mathrm{A}$ (a) Graph $f$ in the window $[0,25]$ by $[40,90]$. (b) Determine the amplitude, period, phase shift, and vertical translation of $f$. (c) What is the average monthly temperature for the month of December? (d) Determine the minimum and maximum average monthly temperatures and the months when they occur (e) What would be an approximation for the average annual temperature in San Antonio? How is this related to the vertical translation of the sine function in the formula for $f$ ? 14. Spring Motion The position of a weight altached to a spring is $s(t)=?4\cos 8?t\text{ inches after }t\text{ seconds. }$ (a) Find the maximum height that the weight rises above the equilibrium position of $s(t)=0$. (b) When does the weight first reach its maximum height if $t?0$ ? (c) What are the frequency and period? 15. Explain why the domains of the tangent and secant functions are the same, and then give a similar explanation for the cotangent and cosecant functions.