(Solved): (1 point) Suppose T : R R is the linear transformation shown in the figure below. 8 7 6 5 ...

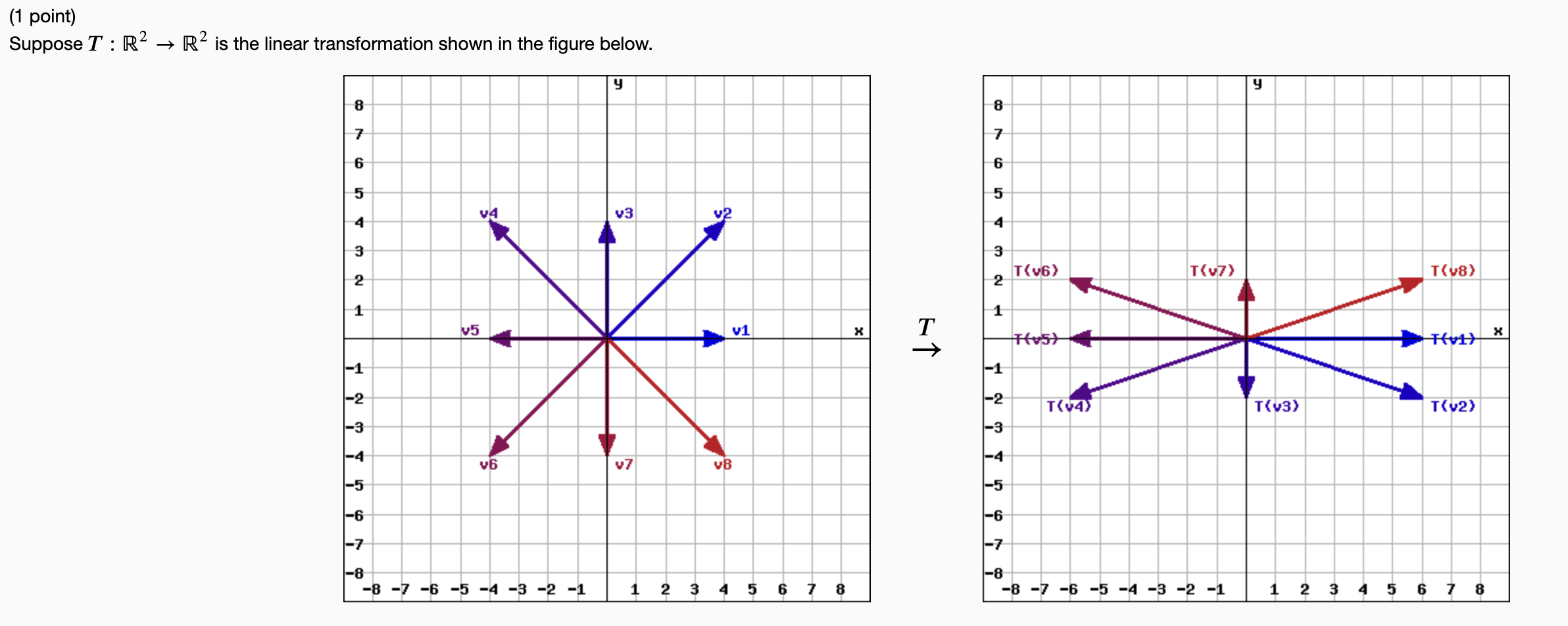
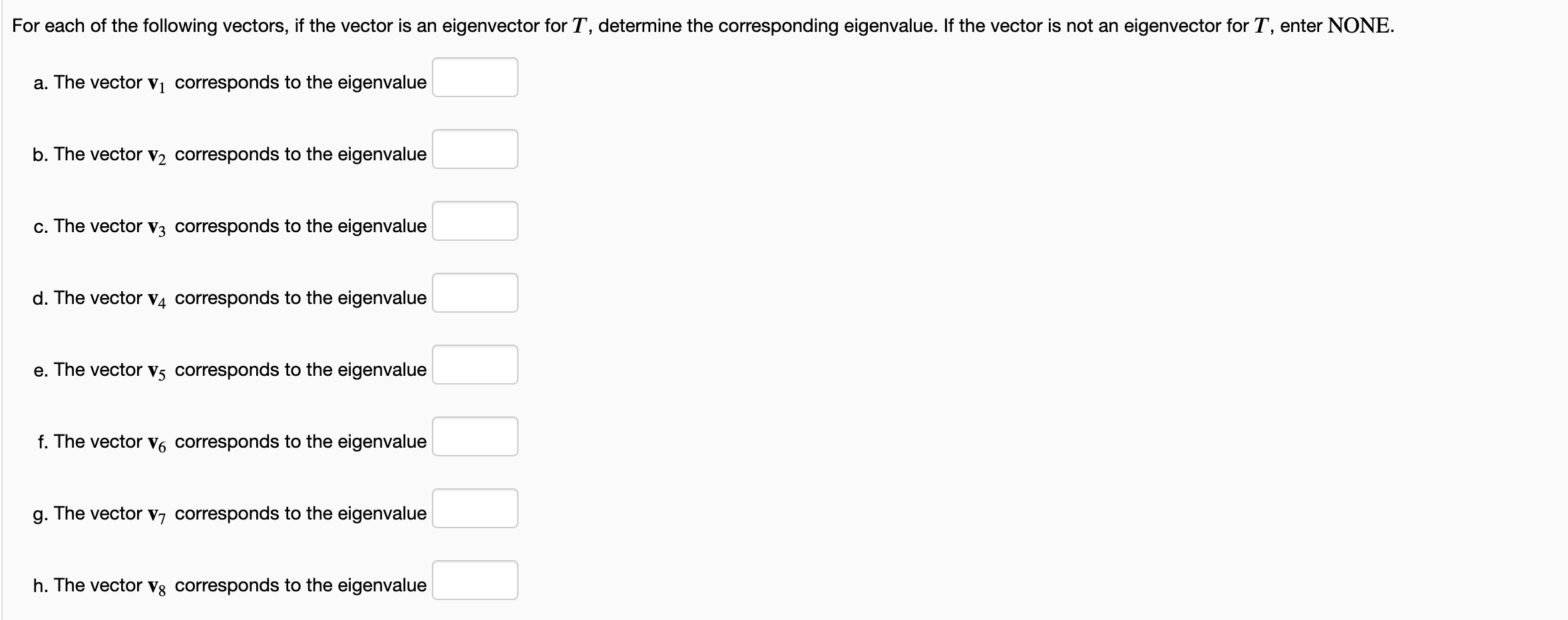
(1 point) Suppose T : R² ? R² is the linear transformation shown in the figure below. 8 7 6 5 NO WA 4 3 2 1 -1 -2 -3 -4 -7 -8 v4 v3 v5 * v1 v7 v6 y -8-7-6 -5 -4 -3 -2 -1 1 2 3 v2 v8 4 5 6 7 8 X T 8 N 7 6 5 4 3 2 1 -1 -2 -3 -4 T(v6) T(v5) T(4) T(v7) -6 -7 -8 -8 -7 -6 -5 -4 -3 -2 -1 y T(v3) 1 2 3 5 T(V8) T(v1) T(v2) 6 7 8 X For each of the following vectors, if the vector is an eigenvector for T, determine the corresponding eigenvalue. If the vector is not an eigenvector for T, enter NONE. a. The vector V? corresponds to the eigenvalue b. The vector v? corresponds to the eigenvalue c. The vector V3 corresponds to the eigenvalue d. The vector v4 corresponds to the eigenvalue e. The vector v5 corresponds to the eigenvalue f. The vector V6 corresponds to the eigenvalue g. The vector V?7 corresponds to the eigenvalue h. The vector v8 corresponds to the eigenvalue Which of the following vectors are eigenvectors for the linear transformation T? Select all correct answers. A. (4,4) B. (8,0) c. (0,0) D. (5,-5) E. (0, -6) Which of the following sets is a basis for the eigenspace E_0.5 of T'? ? A. {(0, 1)) ? B. {(1, 1)) O C. {(1, 1)) ? D. {(1,0)} Which of the following sets is a basis for the eigenspace E1.5 of T? ? A. {(1,0)) ? B. {{-1, 1)) ? C. {(0, 1)) O D. {(1, 1))