1 Two phase equilibrium We consider a system with two phases j= alpha , beta having the mole fractions n^( alpha ),n^( beta ) where the total amount is n_(A)+n_(B). Each component i=A,B in both phases can be described by a chemical potential mu _(i)^(j) and its corresponding mole fraction n_(i)^(j). For the thermodynamic equilibrium the free enth solutionspile.com

Question

1 Two phase equilibrium We consider a system with two phases

j=\alpha ,\beta

having the mole fractions

n^(\alpha ),n^(\beta )

where the total amount is

n_(A)+n_(B)

. Each component

i=A,B

in both phases can be described by a chemical potential

\mu _(i)^(j)

and its corresponding mole fraction

n_(i)^(j)

. For the thermodynamic equilibrium the free enthalpy of the systems is

G=\sum_(i=A) ,B\sum_(j=\alpha ) ,\beta n_(i)^(j)\mu _(i)^(j)

is minimal, with

n_(A)^(\alpha )+n_(A)^(\beta )=n_(A)=

const. and

n_(B)^(\alpha )+n_(B)^(\beta )=n_(B)=

const. Determine the minimum of the total free enthalpy

G

with the constraint of mass conservation. Show that for thermodynamic equilibrium the chemical potentials are identical:

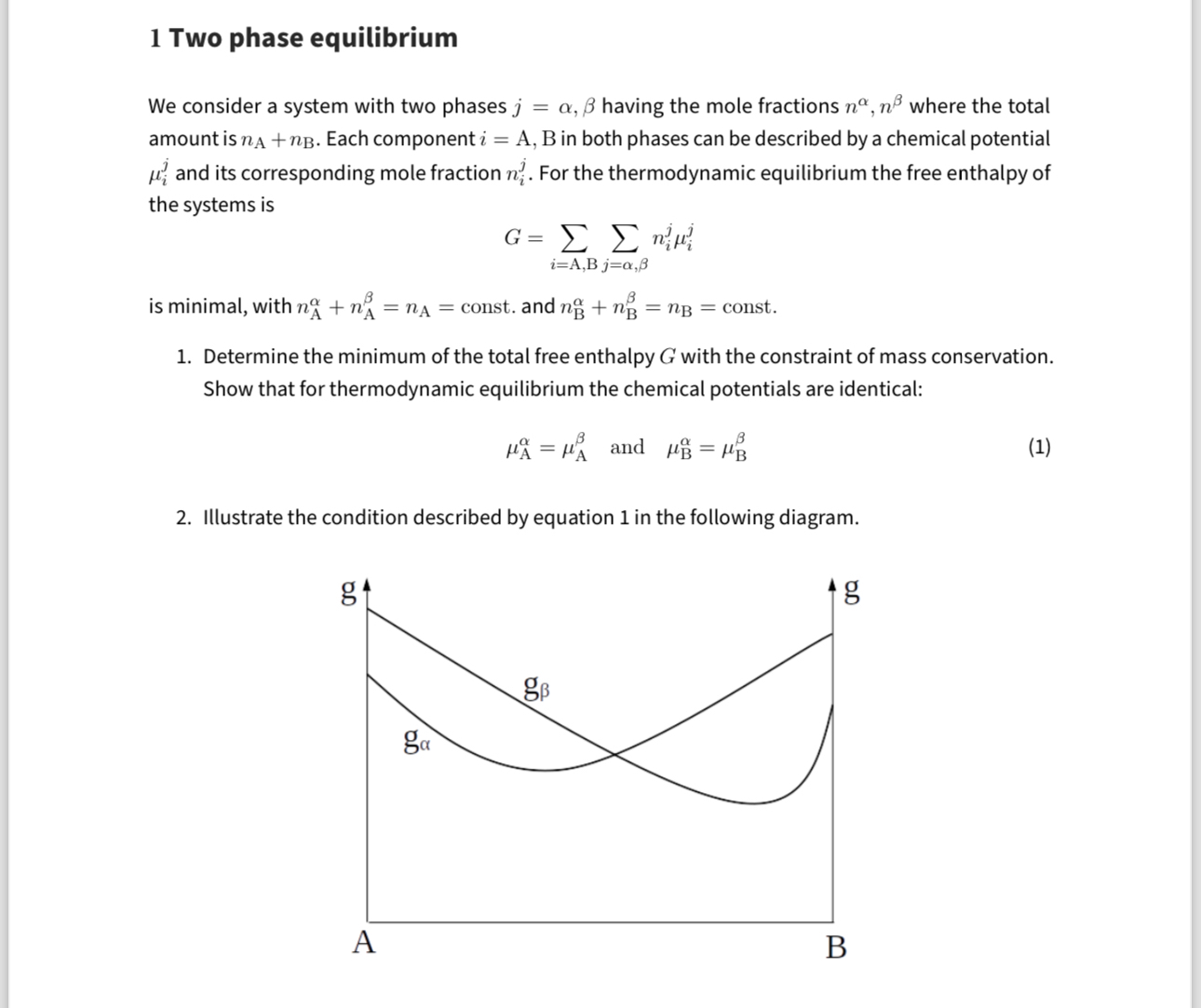
\mu _(A)^(\alpha )=\mu _(A)^(\beta ), and ,\mu _(B)^(\alpha )=\mu _(B)^(\beta )

Illustrate the condition described by equation 1 in the following diagram.

Accepted Answer

Expert Answer to - 1 Two phase equilibrium We consider a system with two phases j= alpha , beta  having the mole fracti

Answer

Solution for - 1 Two phase equilibrium We consider a system with two phases j= alpha , beta  having the mole fracti

Answer

This an additional answer to - 1 Two phase equilibrium We consider a system with two phases j= alpha , beta  having the mole fracti

(Solved): 1 Two phase equilibrium We consider a system with two phases j=\alpha ,\beta having the mole fracti ...