Home /
Expert Answers /
Civil Engineering /
22-a-continuous-steel-beam-in-a-framed-structure-is-to-be-checked-the-bending-moment-mathrm-m-pa422
(Solved): 22. A continuous steel beam in a framed structure is to be checked. The bending moment \( \mathrm{M ...
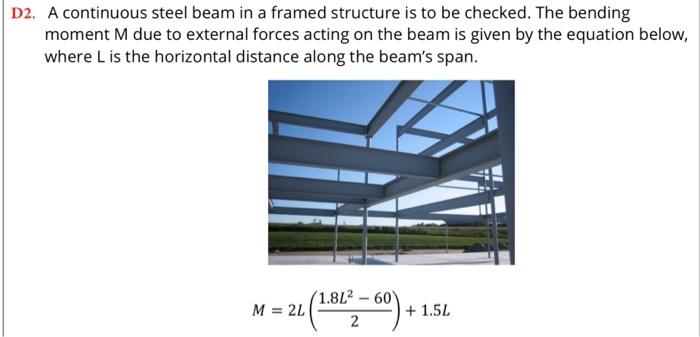
![\[
M=2 L\left(\frac{1.8 L^{2}-60}{2}\right)+1.5 L
\]
Using differential calculus, determine the following:
i. the distance at](https://media.cheggcdn.com/study/242/2424855b-241d-4030-bb68-71c454f829ae/image)
22. A continuous steel beam in a framed structure is to be checked. The bending moment \( \mathrm{M} \) due to external forces acting on the beam is given by the equation below, where \( \mathrm{L} \) is the horizontal distance along the beam's span. \[ M=2 L\left(\frac{1.8 L^{2}-60}{2}\right)+1.5 L \]
\[ M=2 L\left(\frac{1.8 L^{2}-60}{2}\right)+1.5 L \] Using differential calculus, determine the following: i. the distance at which the beam experiences its maximum and minimum bending stress ii. the value of \( L \) when the bending stress is zero. iii. What are the steps in the method for finding the maximum or minimum value of the function? iv. Explain why there might be one point which is a zero of the derivative but not a local maxima or minima. Give examples and support your answer using sketches or diagrams.