(Solved): 2part question need both completed EXAMPLE 2 Find the extreme values of the function f(x,y)=1x2+3y2 ...

EXAMPLE 2 Find the extreme values of the function $$f(x,y)=1x^2+3y^2$$ on the circle $$x^2+y^2=1$$. SOLUTION We are asked for extreme values of $$f$$ subject to the constraint $$g(x,y)=x^2+y^2=1$$. Using Lagrange multipliers, we solve the equations $$?f=??g$$ and $$g(x,y)=1$$, which can be written as $$f_x=?g_x{f}_y=?g_{y}g(x,y)=1$$ or as (1) $$=2x?$$ (2) $$=2y?$$ (3) $$x^2+y^2=1$$ From (1) we have $$x=$$ or $$?=1$$. If $$x=$$, then (3) gives $$y=\pm 1$$. If $$?=1$$, then $$y=$$ from (2), so then (3) gives $$x=\pm 1$$. Therefore $$f$$ has possible extreme values at the points $$(0,1),(0,?1),(1,0)$$, and $$(?1,0)$$. Evaluating $$f$$ at these four points, we find that $$\begin{array}{rl}f(0,1)& =\\ f(0,?1)& =3\\ f(1,0)& =\\ f(?1,0)& =1.\end{array}$$ Therefore the maximum value of $$f$$ on the circle $$x^2+y^2=1$$ is $$f(0,\pm 1)=$$ and the minimum value is $$f(\pm 1,0)=$$ Checking with the figure, we see that these values look reasonable. 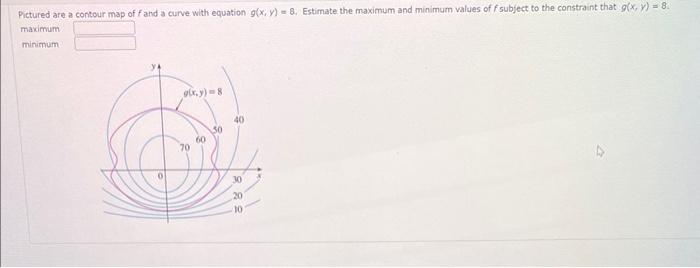Pictured are a contour map of $$f$$ and a curve with equation $$g(x;y)=8$$. Estimate the maximum and minimum values of $$f$$ subject to the constraint that $$g(x,y)=8$$. maximum minitpuim