(Solved): 3. Consider the function \( f(x, y)=3 x- \) \( x^{3}-2 y^{2}+y^{4} \). A contour map is given here. ...

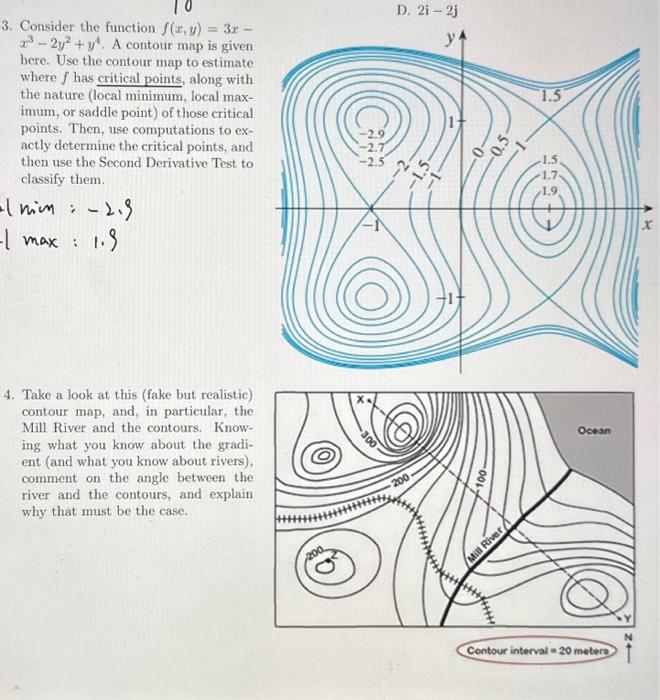
3. Consider the function \( f(x, y)=3 x- \) \( x^{3}-2 y^{2}+y^{4} \). A contour map is given here. Use the contour map to estimate where \( f \) has critical points, along with the nature (local minimum, local maximum, or saddle point) of those critical points. Then, use computations to exactly determine the critical points, and then use the Second Derivative Test to classify them. \( -\min :-2,9 \) \( -\max : 1.9 \) 4. Take a look at this (fake but realistic) contour map, and, in particular, the Mill River and the contours. Knowing what you know about the gradient (and what you know about rivers), comment on the angle between the river and the contours, and explain why that must be the case.