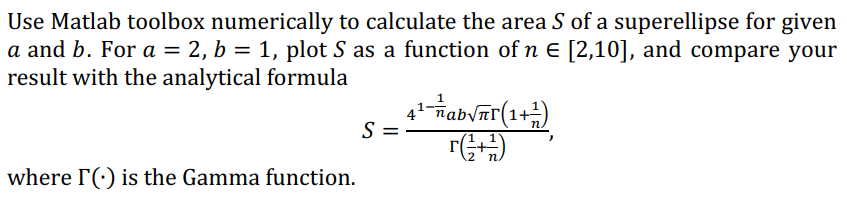(Solved): 4. (20 marks) A superellipse is defined by the inequality axn+by ...

4. (20 marks) A superellipse is defined by the inequality ${?\frac{x}{a}?}^n+{?\frac{y}{b}?}^n?1,$ where $x$ and $y$ are the Cartesian coordinates, and $a$ and $b$ are the length of long and short axes with $n>2$ the deformation parameter. An example of a superellipse centered at ${\mathbf{r}}_0$ with $a=2,b=1$ and $n=2.5$ is shown in the figure below, where ${\mathbf{e}}_x$ and ${\mathbf{e}}_y$ are the unit vectors pointing to the direction of long and short axes, respectively, and ${\mathbf{e}}_x?{\mathbf{e}}_y$. All vectors here are column vectors. Use Matlab toolbox numerically to calculate the area $S$ of a superellipse for given $a$ and $b$. For $a=2,b=1$, plot $S$ as a function of $n?[2,10]$, and compare your result with the analytical formula $S=\frac{4^{1?\frac{1}{n}}ab\sqrt{?}?\left(1+\frac{1}{n}\right)}{?\left(\frac{1}{2}+\frac{1}{n}\right)},$ where $?(?)$ is the Gamma function.