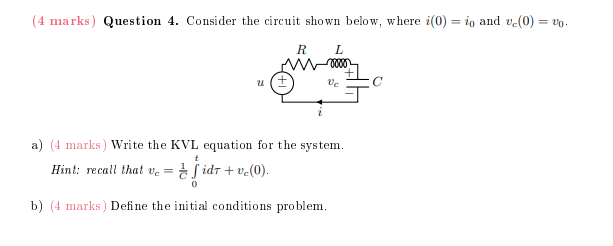
(Solved): (4 marks) Question 4. Consider the circuit shown below, where i(0)=i_(0) and v_(c)(0)=v_(0). a) (4 ...
(4 marks) Question 4. Consider the circuit shown below, where
i(0)=i_(0)and
v_(c)(0)=v_(0). a) (4 marks ) Write the KVL equation for the system. Hint: recall that
v_(c)=(1)/(C)\int_0^t id\tau +v_(c)(0). b) (4 marks ) Define the initial conditions problem. c) (4 marks) Write the problem in Laplace domain. Hint: if you take the Laplace transform of a constant,
K, the result is the same as the Laplace transform of
Kh(t).L{K}=(K)/(s). d) (4 marks) Solve for
I(s). Carefully simplify your solution to the form
I(s)=U(s)(N_(1)(s))/(P_(1)(s))+
(N_(2)(i_(0),v_(0),s))/(P_(2)(s)), where
N_(1),N_(2),P_(1),P_(2)are polynomial functions of
s,N_(2)may also depend on
i_(0)and
v_(0), and
U(s)is the Laplace Transformation of
u(t). e) (2 marks) What is the relationship between
P_(1)and
P_(2)? f) (20 marks) Use Simulink or any other simulation software you are familiar with to construct a simulation model of the system above. Consider the following cases: \table[[Parameter,Case 1,Case 2,Case 3,Case 4],[L,1,1,1,1],[C,1,1,1,1],[R,4,4,1,1],[i_(0),0,5,0,5],[v_(0),0,0,0,0],[u,h(t),0,h(t),0]] For each case answer the following: i. What are the roots of the polynomial
P_(1)(s)for
sinC, where
Cis the set of complex numbers? ii. Find an expression for
i(t)that is valid for
t>0. iii. Plot your solution and the output of the simulations. Hint: They should be exactly the same. Consider using dashed lines to make your result visible. g) (2 marks) What happens when the roots of
P_(1)(s)have non-zero imaginary part?