(Solved): (4 points) Match each of the Maclaurin series with the function it represents. 1. \( \sum_{n=0}^{\ ...

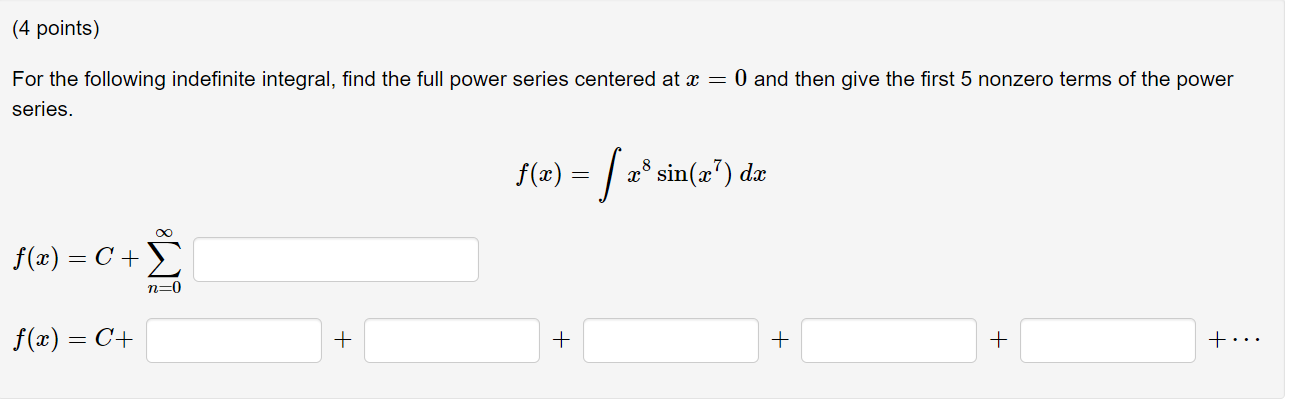
(4 points) Match each of the Maclaurin series with the function it represents. 1. \( \sum_{n=0}^{\infty} \frac{(-1)^{n} x^{2 n+1}}{2 n+1} \) 2. \( \sum_{n=0}^{\infty} \frac{(-1)^{n} x^{2 n}}{(2 n) !} \) 3. \( \sum_{n=0}^{\infty}(-1)^{n} \frac{x^{2 n+1}}{(2 n+1) !} \) 4. \( \sum_{n=0}^{\infty} \frac{x^{n}}{n !} \) A. \( \sin (x) \) B. \( \arctan (x) \) C. \( e^{x} \) D. \( \cos (x) \) For the following indefinite integral, find the full power series centered at \( x=0 \) and then give the first 5 nonzero terms of the power series. \[ f(x)=\int x^{8} \sin \left(x^{7}\right) d x \] \[ f(x)=C+\sum_{n=0}^{\infty} \]