(Solved): 6.30 writing a vector as linear combination of orthonormal basis Suppose e1,,en is an orth ...

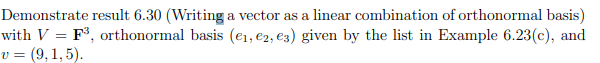
6.30 writing a vector as linear combination of orthonormal basis Suppose $e_1,\dots ,e_n$ is an orthonormal basis of $V$ and $v,w?V$. Then (a) $v=?v,e_1?e_1+?+?v,e_n?e_n$, (b) $?v{?}^2={??v,e_1??}^2+?+{??v,e_n??}^2$ (c) $?v,w?=?v,e_1?\overline{?w,e_1?}+?+?v,e_n?\overline{?w,e_n?}$. Proof Because $e_1,\dots ,e_n$ is a basis of $V$, there exist scalars $a_1,\dots ,a_n$ such that $v=a_1{e}_1+?+a_n{e}_n.$ Because $e_1,\dots ,e_n$ is orthonormal, taking the inner product of both sides of this equation with $e_k$ gives $?v,e_k?=a_k$. Thus 6.30 (a) holds. Now 6.30(b) follows immediately from 6.30(a) and 6.24. Taking the inner product of each side of 6.30 (a) with $w$ and then using the equation $?e_k,w?=\overline{?w,e_k?}$ gives 6.30(c). 6.23 example: orthonormal lists (a) The standard basis of ${\mathbf{F}}^n$ is an orthonormal list. (b) $\left(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}\right),\left(?\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0\right)$ is an orthonormal list in ${\mathbf{F}}^3$. (c) $\left(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}\right),\left(?\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0\right),\left(\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}},?\frac{2}{\sqrt{6}}\right)$ is an orthonormal list in ${\mathbf{F}}^3$. Demonstrate result 6.30 (Writing a vector as a linear combination of orthonormal basis) with $V={\mathbf{F}}^3$, orthonormal basis $\left(e_1,e_2,e_3\right)$ given by the list in Example $6.23(\mathrm{c})$, and $v=(9,1,5)$