Home /
Expert Answers /
Statistics and Probability /
9-3-in-the-approximation-of-the-random-variable-y-by-x-one-may-use-the-mean-cost-e-g-y-pa855
(Solved): 9.3 In the approximation of the random variable Y by (X), one may use the mean cost E{g[Y ...
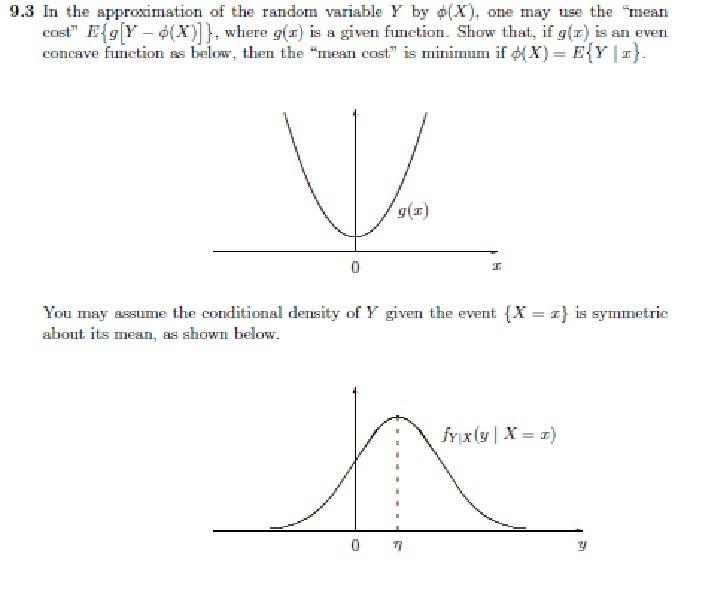
9.3 In the approximation of the random variable by , one may use the mean cost , where is a given function. Show that, if is an even concave function as below, then the "mean cost" is minimum if . You may assume the conditional density of given the event is symmetric abont its mean, as shown below.