(Solved): A. Binary To Decimal The second column of the table below provides an eight-bit binary value. The f ...

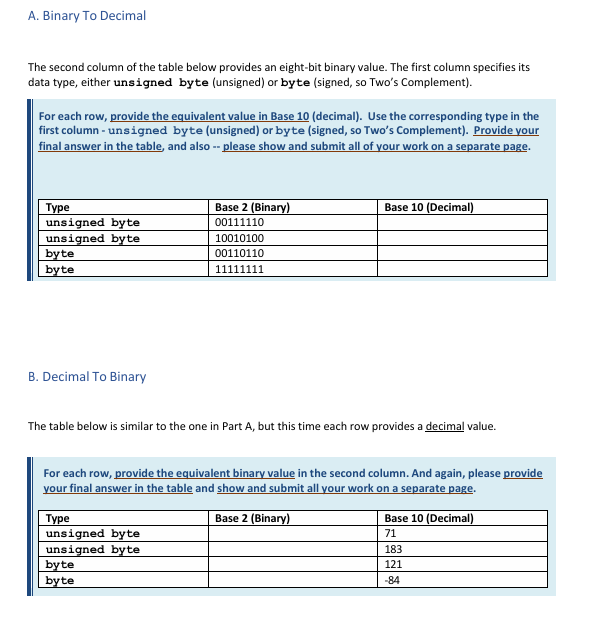
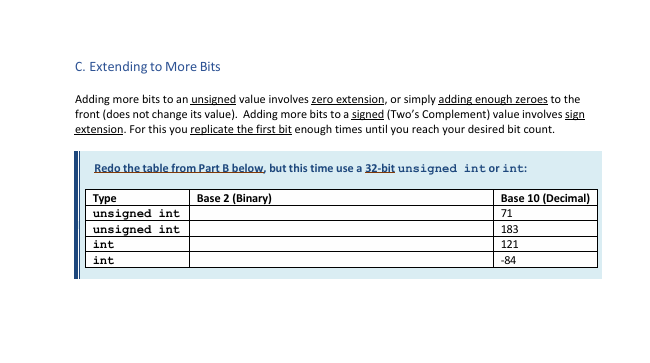
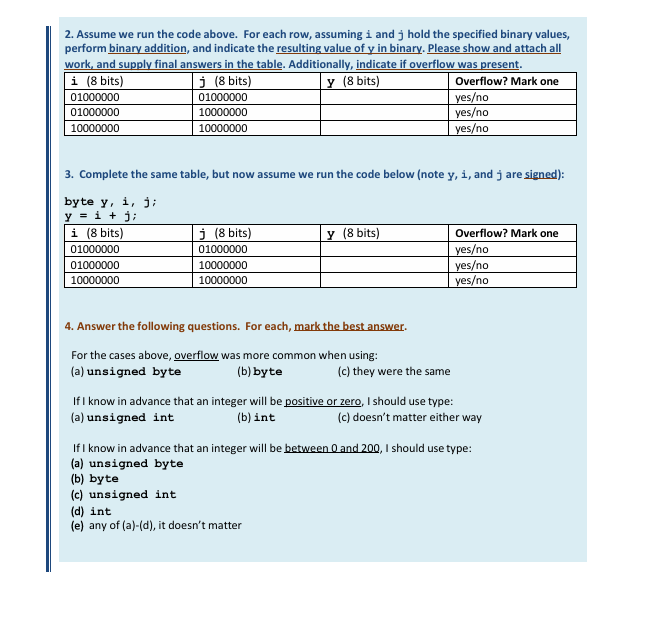
A. Binary To Decimal The second column of the table below provides an eight-bit binary value. The first column specifies its data type, either unsigned byte (unsigned) or byte (signed, so Two's Complement). For each row, provide the equivalent value in Base 10 (decimal). Use the corresponding type in the first column - unsigned byte (unsigned) or byte (signed, so Two's Complement). Provide your final answer in the table, and also -- please show and submit all of your work on a separate page. B. Decimal To Binary The table below is similar to the one in Part A, but this time each row provides a decimal value. For each row, provide the equivalent binary value in the second column. And again, please provide your final answer in the table and show and submit all your work on a separate page. C. Extending to More Bits Adding more bits to an unsigned value involves zero extension, or simply adding enough zeroes to the front (does not change its value). Adding more bits to a signed (Two's Complement) value involves sign extension. For this you replicate the first bit enough times until you reach your desired bit count. Redo the table from Part B below, but this time use a 32 -bit unsigned int or int: A value that is outside the range of the minimum and maximum above, for any of these datatypes, causes overflow. Overflow can sometimes happen inadvertently, when you try to add two values that are in range but your result is out of range. Take the code below: unsigned byte \( y, i, j \); \[ y=i+j \] The variables \( y, i \), and \( j \) are all "unsigned byte" and use the same number of bits. If \( i \) and \( j \) are in the acceptable range for an unsigned byte, but their sum is out of range, y will overflow. Overflow is handled differently in unsigned vs. signed addition. In unsigned addition, overflow happens if there is an extra carry bit on the left. In signed addition, we immediately drop any extra carry bits on the left, and check the signs of our operands and the sign of our result. If we add two positives and get a negative, or two negatives and get a positive, we overflow. We will now test some of these "boundary" cases. 2. Assume we run the code above. For each row, assuming i and \( j \) hold the specified binary values, perform binary addition, and indicate the resulting value of \( y \) in binary. Please show and attach all work, and supply final answers in the table. Additionally, indicate if overflow was present. 3. Complete the same table, but now assume we run the code below (note \( y, i \), and \( j \) are signed): byte \( \mathrm{y}, \mathrm{i}, \mathrm{j} \); \[ y=i+j \] 4. Answer the following questions. For each, mark the best answer. For the cases above, overflow was more common when using: (a) unsigned byte (b) byte (c) they were the same If I know in advance that an integer will be positive or zero, I should use type: (a) unsigned int (b) int (c) doesn't matter either way If I know in advance that an integer will be between 0 and 200, I should use type: (a) unsigned byte (b) byte (c) unsigned int (d) int (e) any of (a)-(d), it doesn't matter