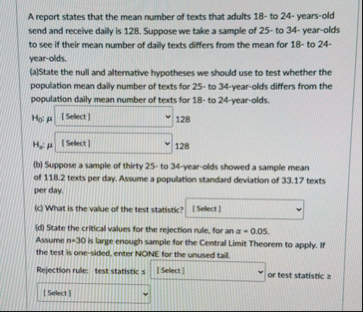
(Solved): A report states that the mean number of texts that adults 18 - to 24 -years-old send and receive dai ...
A report states that the mean number of texts that adults 18 - to 24 -years-old send and receive daily is 128 . Suppose we take a sample of 25 - to 34 - year-olds to see if their mean number of daily texts differs from the mean for 18- to 24-year-olds. (a)State the null and alternative hypotheses we should use to test whether the population mean daily number of texts for 25 - to 34 -year-olds differs from the population daily mean number of texts for 18 - to 24 -year-olds.
H_(0):\mu
?128
H_(2);\mu
?128 (b) Suppose a sample of thirty 25 - to 34 -year-olds showed a sample mean of 118.2 texts per day. Assume a population standard deviation of 33.17 texts per day. (c) What is the value of the test statistic?
?(d) State the critical values for the rejection rule, for an
\alpha =0.05. Assume n-30 is large enough sample for the Central Limit Theorem to apply. If the test is one-sided, enter NONE for the unused tail. Rejection rule: test statistic:
?or test statistic z