(Solved): a. Report the regression equation, using the words "Height" and "Armspan," not \( x \) and \( y \) ...

a. Report the regression equation, using the words "Height" and "Armspan," not \( x \) and \( y \). A. Predicted Height \( =-186.20+2.12 \) Armspan B. Predicted Height \( =2.12-186.20 \) Armspan C. Predicted Armspan \( =2.12-186.20 \) Height D. Predicted Armspan \( =-186.20+2.12 \) Height b. Determine the corresponding values and verify the slope by using the formula \( b_{1}=r \frac{s_{y}}{s_{x}} \). 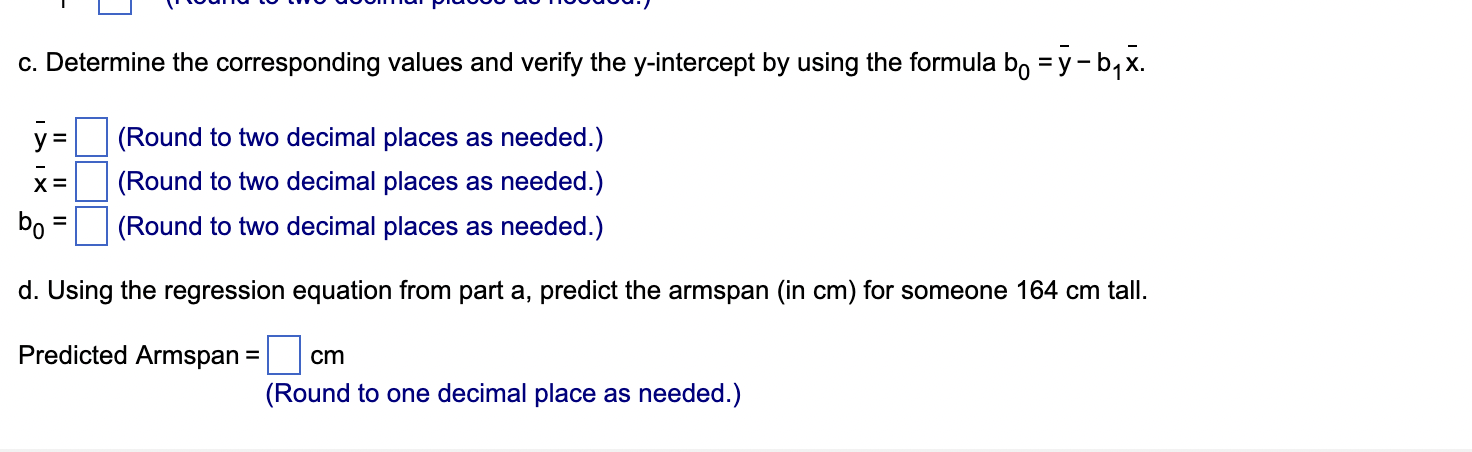c. Determine the corresponding values and verify the \( y \)-intercept by using the formula \( b_{0}=\bar{y}-b_{1} \bar{x} \). \( \bar{y}=\quad \) (Round to two decimal places as needed.) \( \overline{\mathrm{x}}= \) (Round to two decimal places as needed.) \( \mathrm{b}_{0}=\quad \) (Round to two decimal places as needed.) d. Using the regression equation from part a, predict the armspan (in cm) for someone \( 164 \mathrm{~cm} \) tall. Predicted Armspan \( =\quad \mathrm{cm} \) (Round to one decimal place as needed.)