(Solved): As shown on the figure on the right, a grounded conducting plane with a hemispherical bump of radius ...

As shown on the figure on the right, a grounded conducting plane with a hemispherical bump of radius a is placed in an electric field that is asymptotically uniform and perpendicular to the plane. Find the surface charged density everywhere on the conducting surface. Hint: Try using the potential in example 3.8.
I have included the diagram and example 3.8.

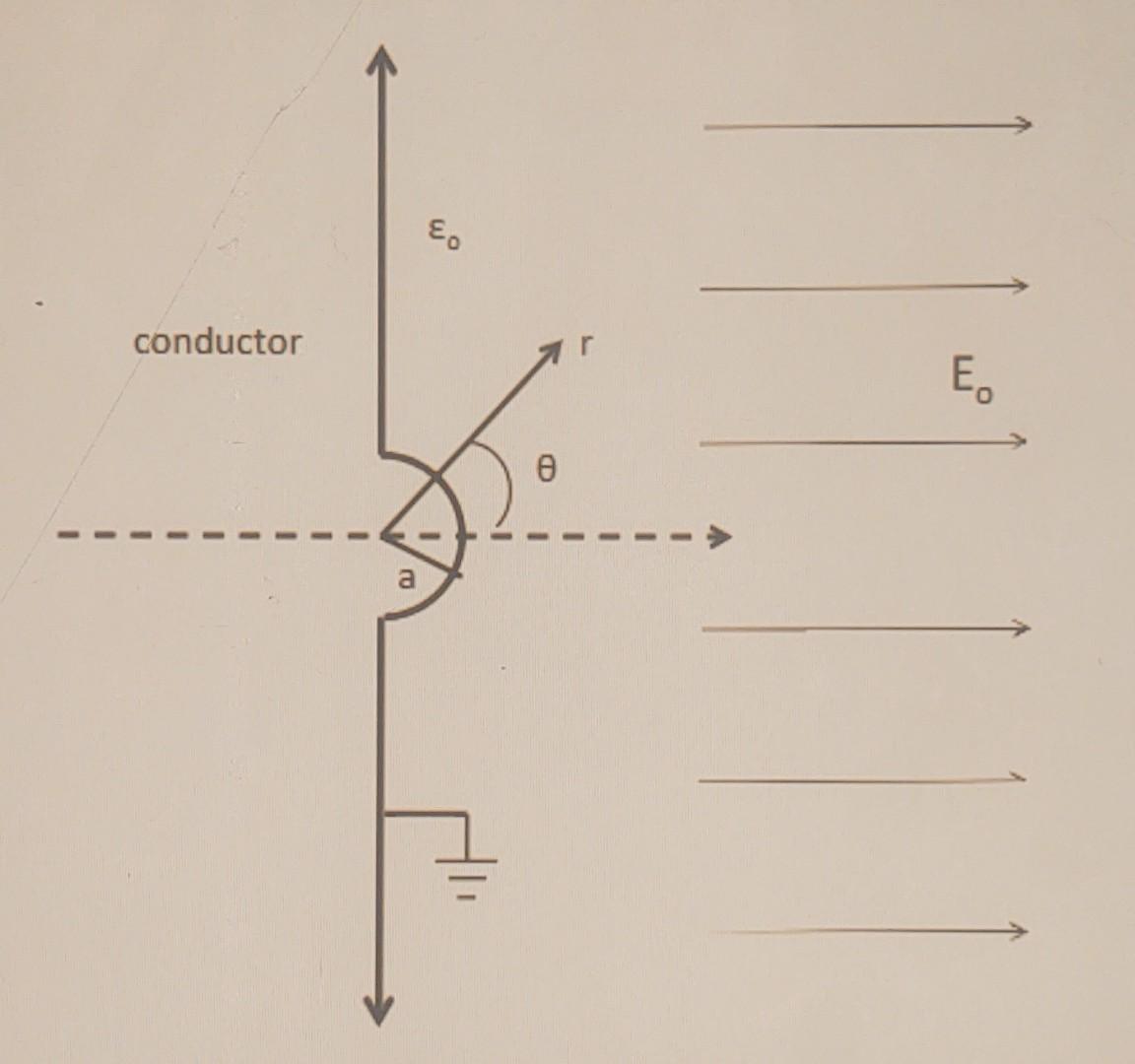
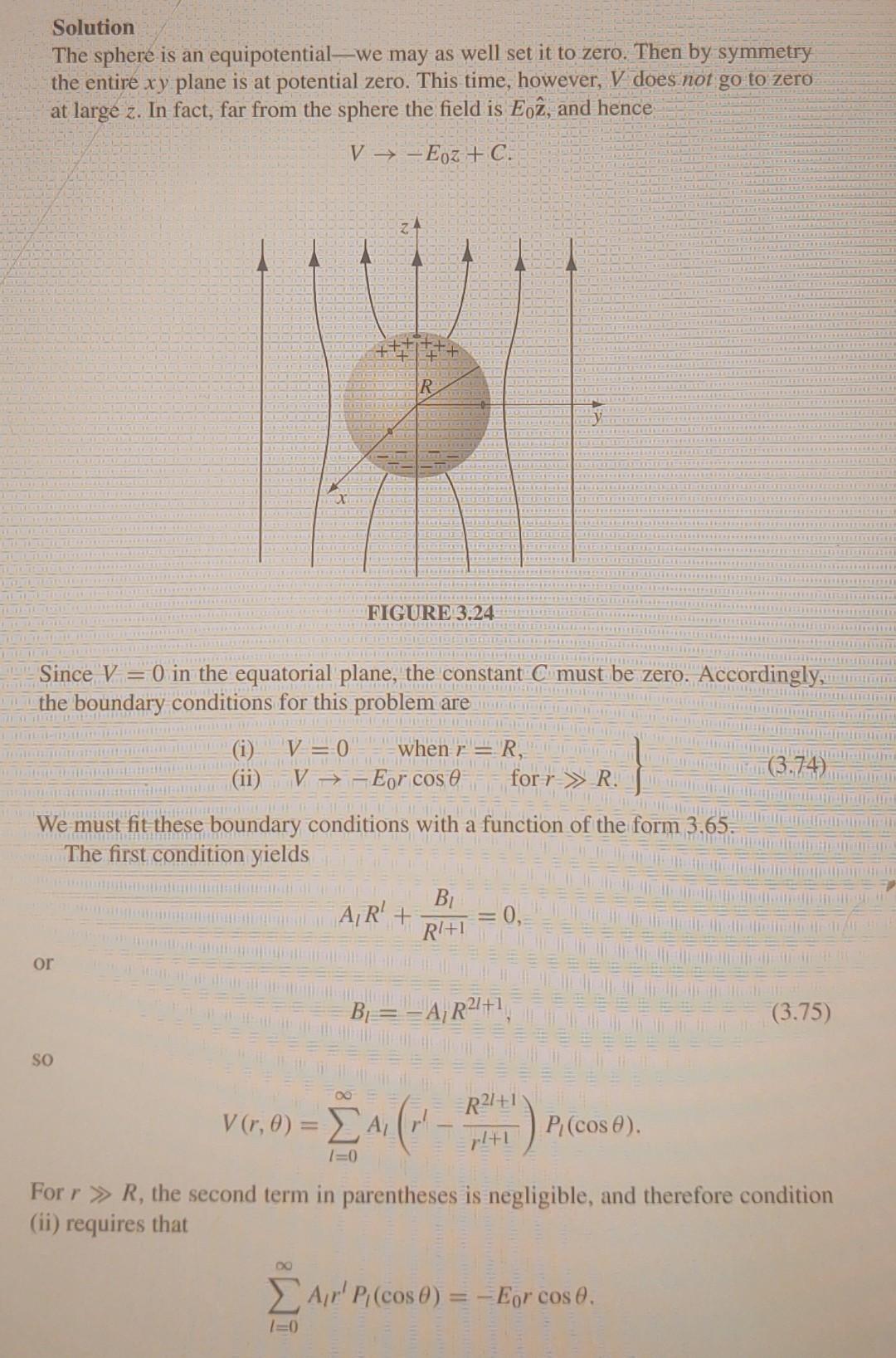
3. As shown in the figure on the right, a grounded conducting plane with a hemispherical bump of radius $a$ is placed in an electric field that is asymptotically uniform and perpendicular to the plane. Find the surface charge density everywhere on the conducting surface. Hint: Try using the potential in Example 3.8. Solution The sphere is an equipotential-we may as well set it to zero. Then by symmetry the entire $xy$ plane is at potential zero. This time, however, $V$ does not go to zero at large $z$. In fact, far from the sphere the field is $E_0\hat{\mathbf{z}}$, and hence $V??E_{0}z+C$ FIGURE 3.24 Since $V=0$ in the equatorial plane, the constant $C$ must be zero. Accordingly, the boundary conditions for this problem are (i) $V=0$ when $r=R$, (ii) $V??E_{0}r\cos ?$ for $r?R$. We must fit these boundary conditions with a function of the form 3,65 . The first condition yields $A_l{R}^l+\frac{B_l}{R^{l+1}}=0$ or $B_l=?A_l{R}^{2l+1}$ so $V(r,?)={?}_{l=0}^{?}{A}_l\left(r^l?\frac{R^{2l+1}}{r^{l+1}}\right)P_l(\cos ?).$ For $r?R$, the second term in parentheses is negligible, and therefore condition (ii) requires that ${?}_{l=0}^{?}{A}_l{r}^l{P}_l(\cos ?)=?E_{0}r\cos ?$ Example 3.8. An uncharged metal sphere of radius $R$ is placed in an otherwise uniform electric field $\mathbf{E}=E_0\hat{\mathbf{z}}$. The field will push positive charge to the "northern" surface of the sphere, and-symmetrically-negative charge to the "southern" surface (Fig. 3.24). This induced charge, in turn, distorts the field in the neighborhood of the sphere. Find the potential in the region outside the sphere. Evidently only one term is present: $l=1$. In fact, since $P_1(\cos ?)=\cos ?$, we can read off immediately $A_1=?E_0,\text{ all other }{A}_l\text{ ’s zero. }$ Conclusion: $V(r,?)=?E_0\left(r?\frac{R^3}{r^2}\right)\cos ?.$ The first term $\left(?E_{0}r\cos ?\right)$ is due to the external field; the contribution attributable to the induced charge is $E_0\frac{R^3}{r^2}\cos ?$ If you want to know the induced charge density, it can be calculated in the usual way: $?(?)=?{{?}_0\frac{?V}{?r}?}_{r=R}={{?}_0{E}_0\left(1+2\frac{R^3}{r^3}\right)\cos ??}_{r=R}=3{?}_0{E}_0\cos ?.$ As expected, it is positive in the "northern" hemisphere $(0????/2)$ and negative in the "southern" $(?/2????)$.