(Solved): Assume \( \mathrm{p}=0.42 \) Q1. The expected average and standard error of \( \hat{p} \) for a sa ...

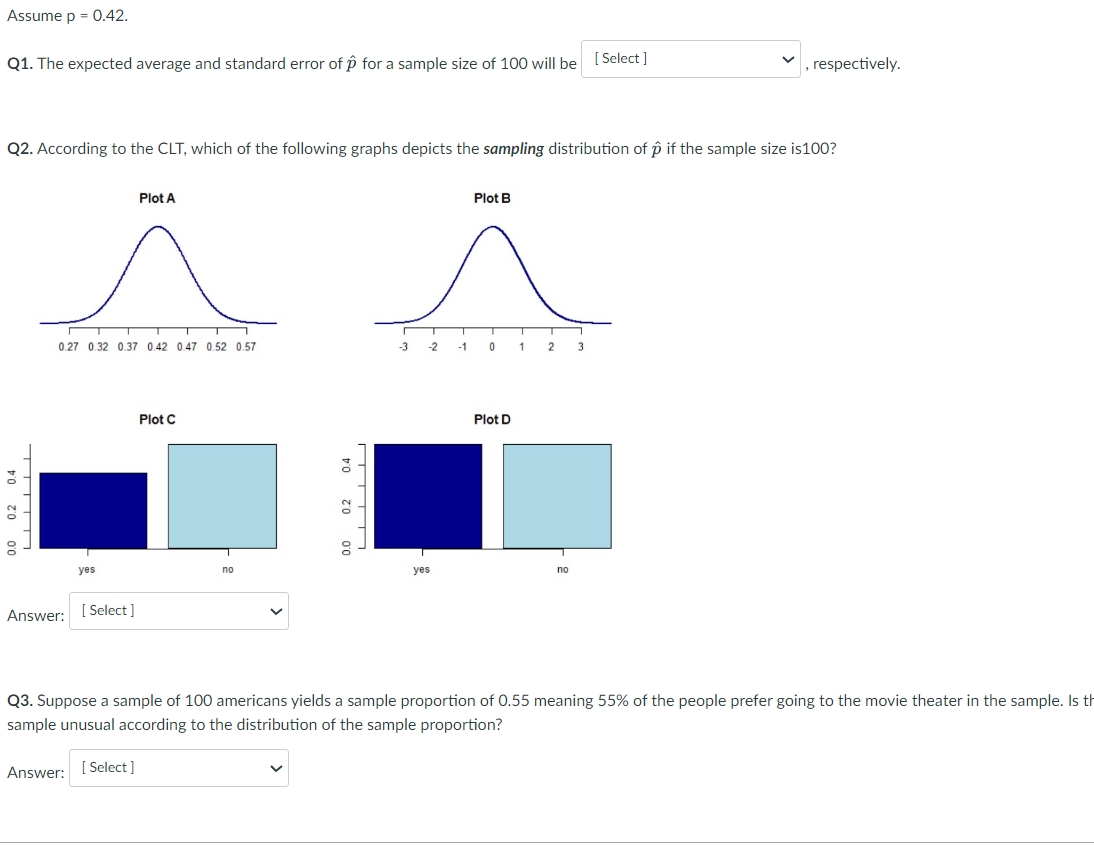
Assume \( \mathrm{p}=0.42 \) Q1. The expected average and standard error of \( \hat{p} \) for a sample size of 100 will be , respectively. Q2. According to the CLT, which of the following graphs depicts the sampling distribution of \( \hat{p} \) if the sample size is100? Answer: Q3. Suppose a sample of 100 americans yields a sample proportion of 0.55 meaning \( 55 \% \) of the people prefer going to the movie theater in the sample. Is th sample unusual according to the distribution of the sample proportion? Answer: a hypothesis test that could be used to test the claim on the label. The hypotheses are: \( H_{0}: \mu=2 \) grams of carbohydrates \( H_{a}: \mu>2 \) grams of carbohydrates Q1. For each of the following possible outcomes when would we make the 'correct" choice and when would we make a Type I or Type II error. Outcome A. - Result: We get a small \( p \)-value and reject the null. - Decision: We assume the label is wrong and the powder contains an average of more than 2 grams of carbs. - Realty: The label is incorrect and the actual average carbs per serving is more than 2 grams. Outcome B. - Result: We get a small p-value and reject the null. - Decision: We assume the label is wrong and the powder contains an average of more than 2 grams of carbs. - Realty: The label is correct and the actual average carbs per serving is 2 grams (or fewer). Outcome C. - Result: We get a large p-value and fail to reject the null. - Decision: We support the claim on the label that the powder contains an average of 2 grams of carbs. - Realty: The label is correct and the actual average carbs per serving is 2 grams (or fewer). Outcome D. - Result: We get a large p -value and fail to reject the null. - Decision: We support the claim on the label that the powder contains an average of 2 grams of carbs. - Reality: The label is incorrect and the actual average carbs per serving is more than 2 grams. Q2. Which consequences correspond to making a Type I Error or Type I Error in this case? Consequence A . This error would claim that the product is not meeting its label specification when it really is meeting its specification. This could result in an unnecessary and costly recall. Consequence \( \mathbf{B} \). This error would miss the fact that the product is not meeting its label specification. This could result in upset customers due to a higher cart amount than anticipated.