(Solved): C PROGRAMMING HELP   Reporting the Error For this program you will report the error as a perc ...

C PROGRAMMING HELP

 

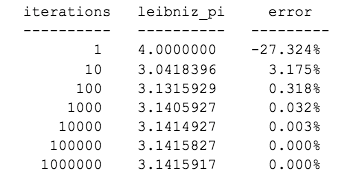
Reporting the Error For this program you will report the error as a percentage in the table. That can be done like this: Take the value for M_PI, subtract the estimate you got from leibniz_pi. That's the actual error. Divide byM_PI. That's the error as a proportion of the best estimate for \( \pi \) we have in the C Standard Library. Now multiply times 100 to make it a percent. There ya go. - Has a main () function and another function that has this prototype: double leibniz_pi(int iterations); What the function does will be discussed below. - The main () function will call leibniz_pi () with various values for iterations. Each time, leibniz_pi () will return an estimate for \( \pi \) (pronounced, "pie") based on the Leibniz series discussed below. - The values you will supply to leibniz_pi () for the number of iterations will be powers of 10 , namely these: \( 1,10,100,1000,10000,100000 \), and 1000000 . So that means you're going to make 7 calls total to leibni z_pi (), and one of them might look like, double val = leibniz_pi (10); ...as one example. These calls should be inside a loop in your main () function. - Each value you receive back from leibniz_pi () will be put into an array that you have declared for that purpose. \begin{tabular}{rlr} iterations & leibniz_pi & error \\ \hline 1 & \( 4.0000000 \) & \( -27.324 \% \) \\ 10 & \( 3.0418396 \) & \( 3.175 \% \) \\ 100 & \( 3.1315929 \) & \( 0.318 \% \) \\ 1000 & \( 3.1405927 \) & \( 0.032 \% \) \\ 10000 & \( 3.1414927 \) & \( 0.003 \% \) \\ 100000 & \( 3.1415827 \) & \( 0.000 \% \) \\ 1000000 & \( 3.1415917 \) & \( 0.000 \% \) \end{tabular}