Home /
Expert Answers /
Calculus /
change-the-integral-to-spherical-coordinates-int-2-2-int-0-sqrt-4-x-2-int-sqrt-x-2-pa148
(Solved): Change the integral to spherical coordinates. \int_(-2)^2 \int_0^(\sqrt(4-x^(2))) \int_(\sqrt(x^(2)+ ...
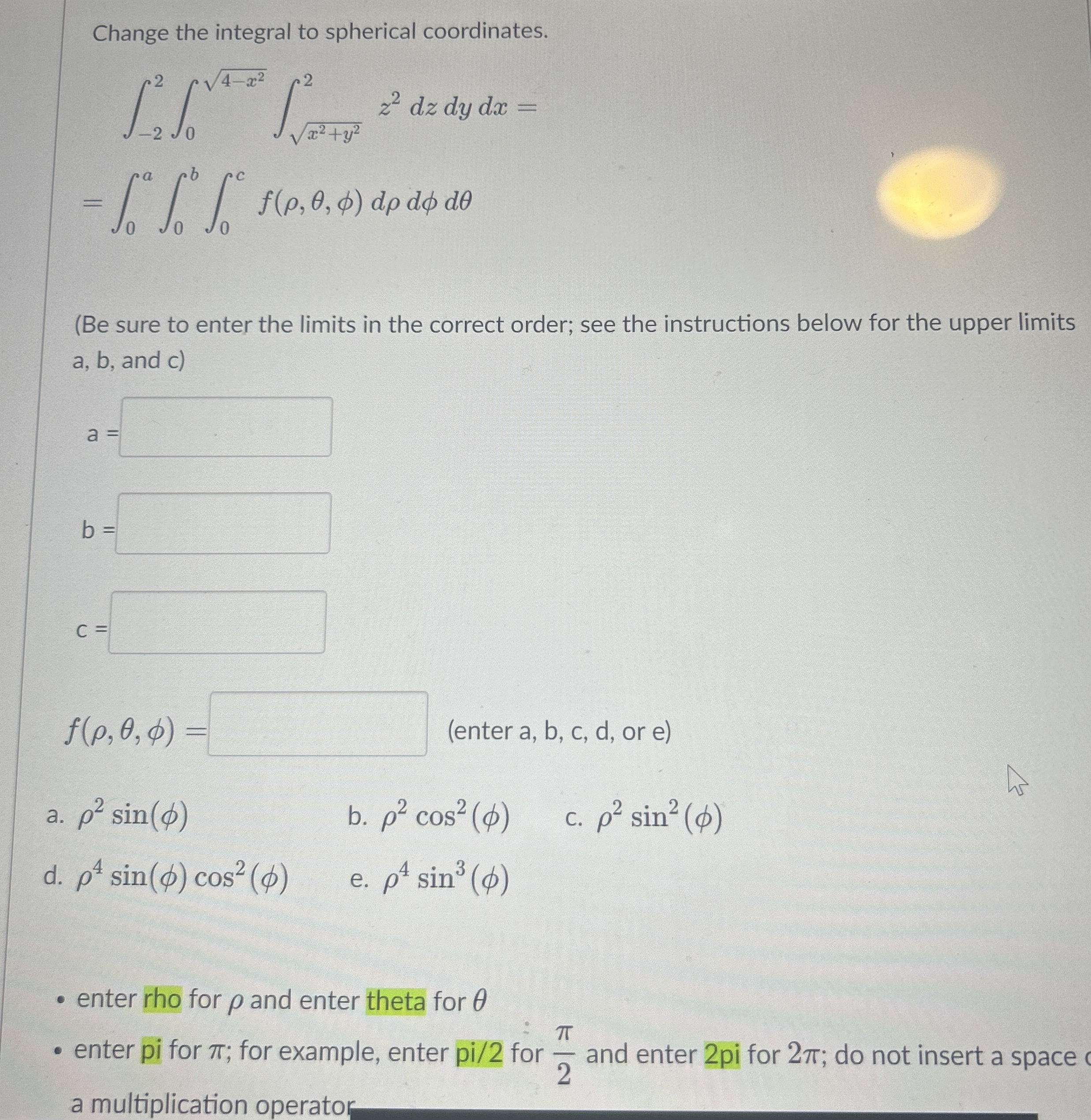
Change the integral to spherical coordinates.
\int_(-2)^2 \int_0^(\sqrt(4-x^(2))) \int_(\sqrt(x^(2)+y^(2)))^2 z^(2)dzdydx=
=\int_0^a \int_0^b \int_0^c f(\rho ,\theta ,\phi )d\rho d\phi d\theta (Be sure to enter the limits in the correct order; see the instructions below for the upper limits a, b, and c)
?
a=
b=
?
c=
?
f(\rho ,\theta ,\phi )=
?(enter
a,b,c,d, or e) a.
\rho ^(2)sin(\phi )b.
\rho ^(2)cos^(2)(\phi )c.
\rho ^(2)sin^(2)(\phi )d.
\rho ^(4)sin(\phi )cos^(2)(\phi )e.
\rho ^(4)sin^(3)(\phi )enter rho for
\rho and enter theta for
\theta enter pi for
\pi ; for example, enter pi/2 for
(\pi )/(2)and enter 2 pi for
2\pi ; do not insert a space a multiplication operator