Home /
Expert Answers /
Civil Engineering /
consider-a-beam-supported-with-a-roller-on-one-end-and-fixed-on-the-other-end-see-the-figure-a-be-pa624
(Solved): Consider a beam supported with a roller on one end and fixed on the other end (see the Figure (a) be ...
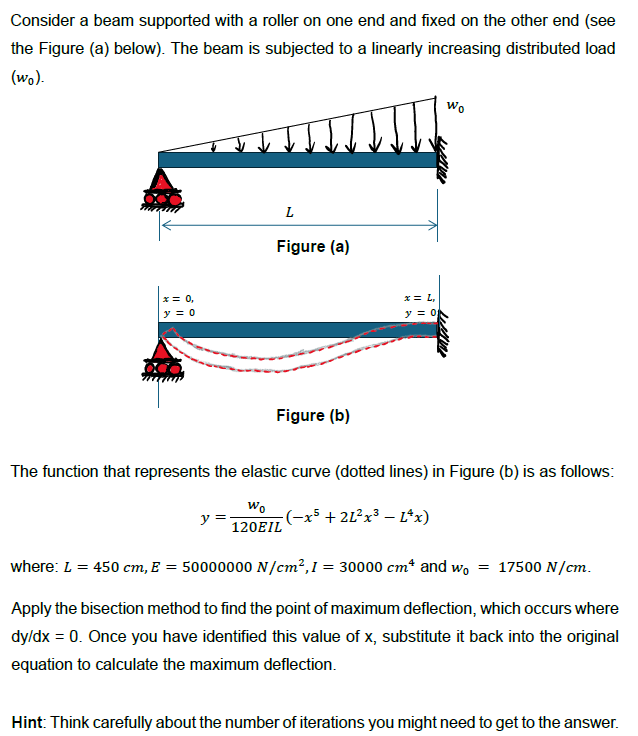
Consider a beam supported with a roller on one end and fixed on the other end (see
the Figure (a) below). The beam is subjected to a linearly increasing distributed load
(w_(0)).
Figure (b)
The function that represents the elastic curve (dotted lines) in Figure (b) is as follows:
y=(w_(0))/(120EIL)(-x^(5)+2L^(2)x^(3)-L^(4)x)
where: L=450cm,E=50000000(N)/(c)m^(2),I=30000cm^(4) and w_(0)=17500(N)/(c)m.
Apply the bisection method to find the point of maximum deflection, which occurs where
d(y)/(d)x=0. Once you have identified this value of x, substitute it back into the original
equation to calculate the maximum deflection.
Hint: Think carefully about the number of iterations you might need to get to the answer. 2.1 Provide the steps to show that the Q-h relationship for the channel can be
represented by the following equation:
Q=(((h^(2)+hcot(\theta ))^((5)/(3)))/(0.014cot(\theta )))((sin(\theta ))/(2h+cos(\theta )))^((2)/(3))(0.009)^(0.5)
Where \theta is the angle of the sides of the channel and hh \theta =
45\deg and you know that h falls between 0.3 and 0.6 m .
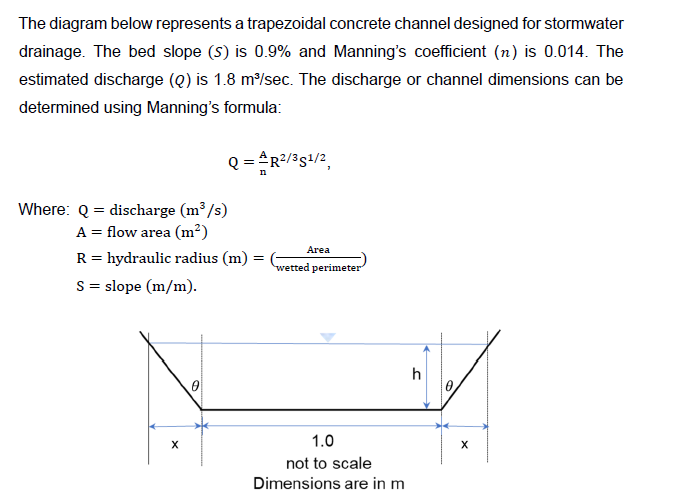
Hint: f(h)=(((h^(2)+hcot(\theta ))^((5)/(3)))/(0.014cot(\theta )))((sin(\theta ))/(2h+cos(\theta )))^((2)/(3))(0.009)^(0.5)-1.8 The diagram below represents a trapezoidal concrete channel designed for stormwater
drainage. The bed slope (S) is 0.9% and Manning's coefficient (n) is 0.014 . The
estimated discharge (Q) is 1.8(m^(3))/(sec). The discharge or channel dimensions can be
determined using Manning's formula:
Q=(A)/(n)R^((2)/(3))S^((1)/(2))
Where: Q=discharge((m^(3))/(s))
A= flow area (m^(2))
R= hydraulic radius (m)=(( Area )/( wetted perimeter ))
S= slope ((m)/(m)). 1.5 Provide the R commands (or any programming tool of your choice) and a
screenshot to show the plot, including a title and labels on the horizontal and vertical
axes, for the following equation:
M=12.5x-0.75x^(3)
x is to be defined from 0 to 5 at an interval of 0.05
Title: Bending Moment Diagram
Horizontal axis label: Distance along the beam (m)
Vertical axis label: Bending Moment (kNm)