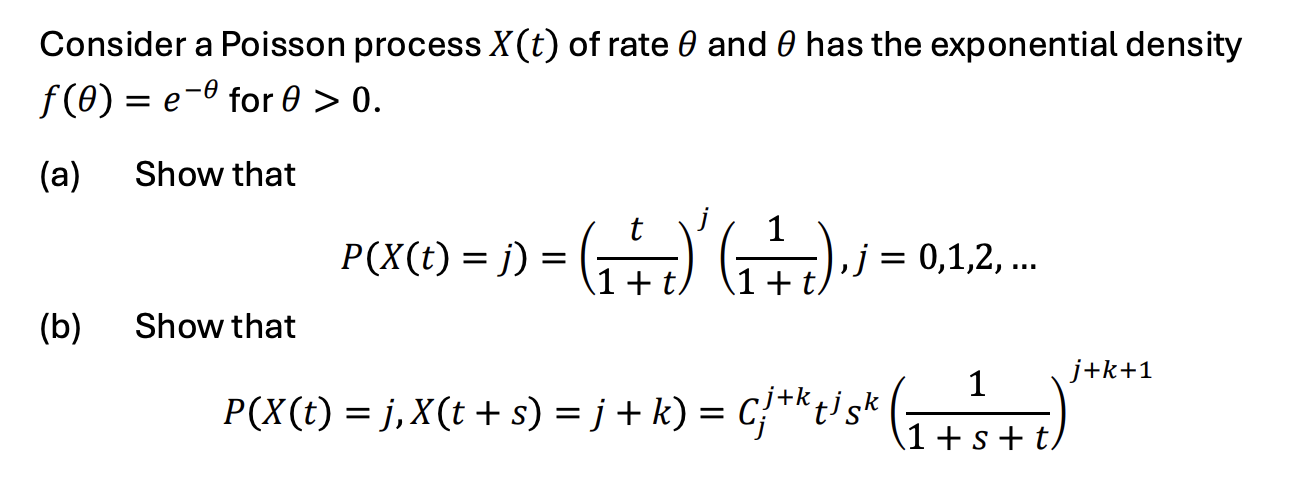Home /
Expert Answers /
Statistics and Probability /
consider-a-poisson-process-x-t-of-rate-theta-and-theta-has-the-exponential-density-f-theta-e-pa617
(Solved): Consider a Poisson process x(t) of rate \theta and \theta has the exponential density f(\theta )=e^( ...
Consider a Poisson process x(t) of rate \theta and \theta has the exponential density
f(\theta )=e^(-\theta ) for \theta >0.
(a) Show that
P(x(t)=j)=((t)/(1+t))^(j)((1)/(1+t)),j=0,1,2,dots
(b) Show that
P(x(t)=j,x(t+s)=j+k)=C_(j)^(j+k)t^(j)s^(k)((1)/(1+s+t))^(j+k+1)