(Solved): Consider an I-beam section with unequal flanges (Figure 2), where \( w_{1}=8 \mathrm{in} \)., \( h=7 ...

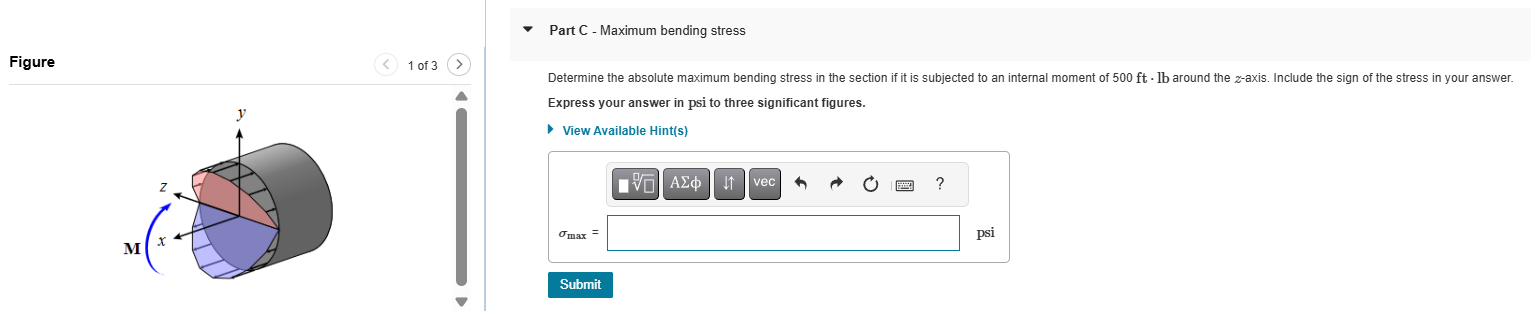
Consider an I-beam section with unequal flanges (Figure 2), where \( w_{1}=8 \mathrm{in} \)., \( h=7.9 \mathrm{in} \)., \( w_{2}=4.5 \mathrm{in} \), \( f=1.25 \mathrm{in} \)., and \( w=0.75 \mathrm{in} \). The beam is subjected to a moment so that the Learning Goal: To find the centroid and moment of inertia of an I-beam's cross section, and to use the flexure formula to find the stress at a point on the cross section due to an internal bending moment. When a beam is subjected to an internal bending moment \( M \) (Figure 1), the stress distribution acting on a cross section can be related to the moment at that section and the geometric properties of the cross section using the flexure formula. The relationship can be written in terms of the maximum stress, \( \sigma_{\max }=\frac{M c}{I} \), where \( c \) is the perpendicular distance from the neutral axis to the farthest point in the section. It can also be written in terms of the vertical distance from the neutral axis, \( y, \sigma=-\frac{M y}{I} \). In each equation, \( I \) is the moment of inertia of the cross-sectional area about the same neutral axis. The neutral axis of the section passes through the centroid. internal moment on the section is about the \( z \)-axis. Part A - Locate the centroid Since the widths of the two flanges are not the same, the centroid is not readily apparent. What is the distance \( \bar{y}^{\prime} \) from the bottom of the section to the centroid? (Figure 3 ) Express your answer with appropriate units to three significant figures. View Available Hint(s) \( \bar{y}^{\prime}= \) Part B - Calculate the moment of inertia Once the position of the centroid is known, the moment of inertia can be calculated. What is the moment of inertia of the section for bending around the \( z \)-axis? Express your answer to three significant figures and include the appropriate units. View Available Hint(s) Part C - Maximum bending stress Figure Determine the absolute maximum bending stress in the section if it is subjected to an internal moment of \( 500 \mathrm{ft} \cdot \mathrm{lb} \) around the \( z \)-axis. Include the sign of the stress in your answer.