(Solved): Consider sampling from two independent populations. Population A has mean \( \mu_{A}=2 \mu \) and ...

Consider sampling from two independent populations. Population A has mean \( \mu_{A}=2 \mu \) and variance \( \sigma_{A}^{2}=\sigma^{2} \) while population B has mean \( \mu_{B}=\mu \) and variance \( \sigma_{B}^{2}=\frac{1}{2} \sigma^{2} \). We are interested in estimating the difference in the population means with two estimators: \[ \begin{aligned} \hat{\theta}_{1} &=\frac{2}{3} \bar{X}_{40}-\frac{1}{3} \bar{Y}_{50} \\ \hat{\theta}_{2} &=\frac{3}{4} \bar{X}_{40}-\frac{1}{2} \bar{Y}_{50} \end{aligned} \] where \( \bar{X}_{40} \) is the sample mean from a size 40 random sample of population \( A \) and \( \bar{Y}_{50} \) is the sample mean from a size 50 random sample of population B. Assume \( \bar{X}_{40} \) and \( \bar{Y}_{50} \) are independent. 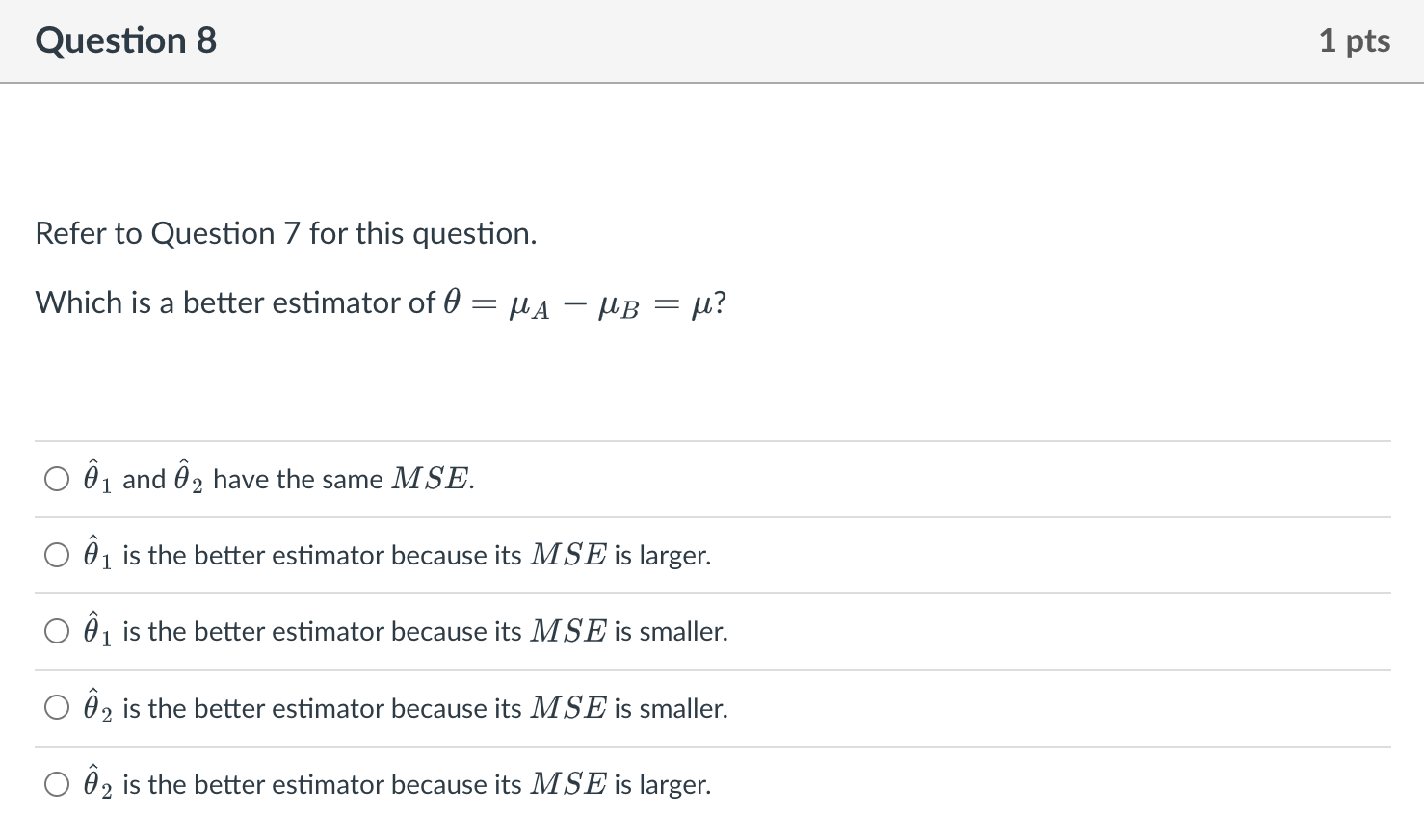Refer to Question 7 for this question. Which is a better estimator of \( \theta=\mu_{A}-\mu_{B}=\mu \) ? \( \hat{\theta}_{1} \) and \( \hat{\theta}_{2} \) have the same \( M S E \). \( \hat{\theta}_{1} \) is the better estimator because its \( M S E \) is larger. \( \hat{\theta}_{1} \) is the better estimator because its \( M S E \) is smaller. \( \hat{\theta}_{2} \) is the better estimator because its \( M S E \) is smaller. \( \hat{\theta}_{2} \) is the better estimator because its \( M S E \) is larger.