(Solved): Consider the following network. With the indicated link costs, use Dijkstra's ...

???????

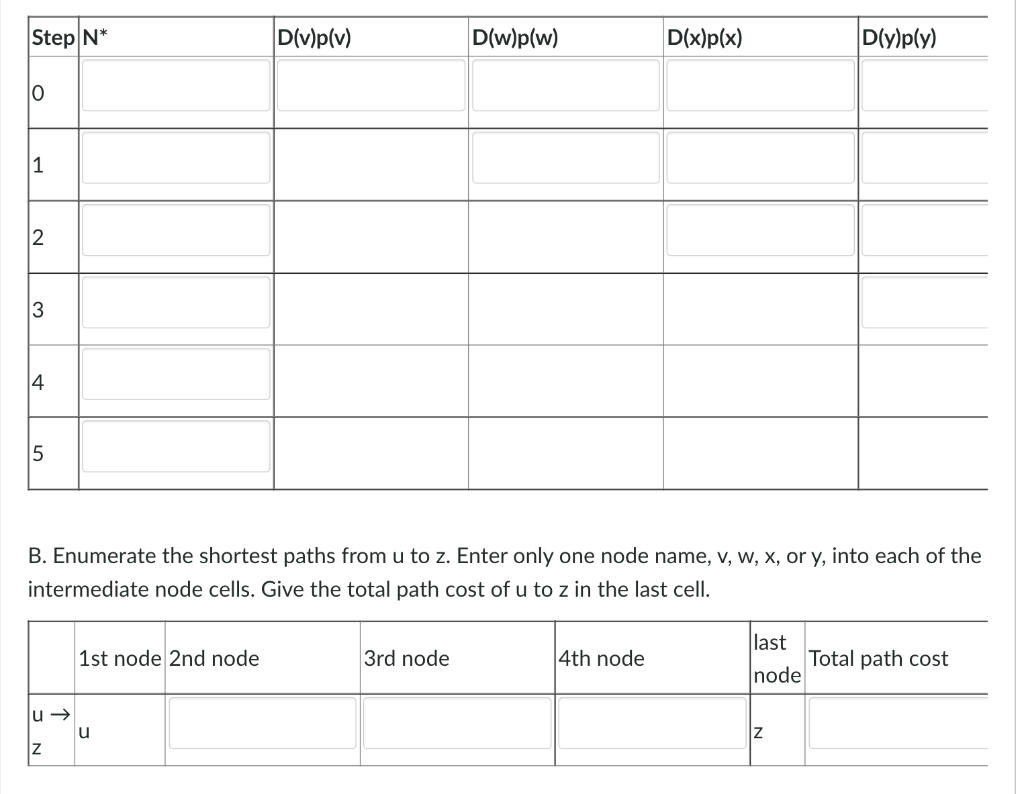
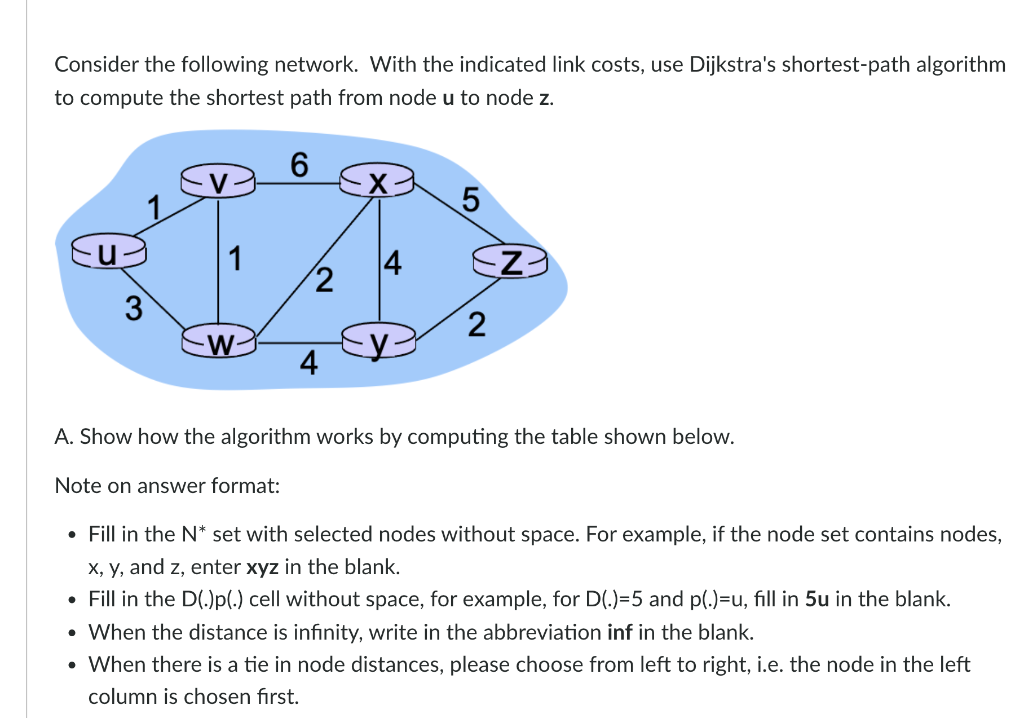
Consider the following network. With the indicated link costs, use Dijkstra's shortest-path algorithm to compute the shortest path from node \( u \) to node \( z \). A. Show how the algorithm works by computing the table shown below. Note on answer format: - Fill in the \( \mathrm{N}^{*} \) set with selected nodes without space. For example, if the node set contains nodes, \( \mathrm{x}, \mathrm{y} \), and \( \mathrm{z} \), enter \( \mathrm{xyz} \) in the blank. - Fill in the \( \mathrm{D}(.) \mathrm{p}( \).\( ) cell without space, for example, for \mathrm{D}()= \).5 and \( \mathrm{p}()=.\mathrm{u} \), fill in \( 5 \mathrm{u} \) in the blank. - When the distance is infinity, write in the abbreviation inf in the blank. - When there is a tie in node distances, please choose from left to right, i.e. the node in the left column is chosen first. B. Enumerate the shortest paths from \( u \) to \( z \). Enter only one node name, \( \mathrm{v}, \mathrm{w}, \mathrm{x} \), or \( \mathrm{y} \), into each of the intermediate node cells. Give the total path cost of \( u \) to \( z \) in the last cell.