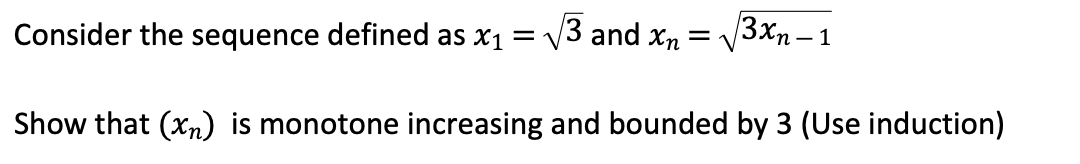Home / Expert Answers / Advanced Math / consider-the-sequence-defined-as-x-1-sqrt-3-and-x-n-sqrt-3-x-n-1-show-that-pa869

(Solved): Consider the sequence defined as \( x_{1}=\sqrt{3} \) and \( x_{n}=\sqrt{3 x_{n-1}} \) Show that \ ...


Consider the sequence defined as \( x_{1}=\sqrt{3} \) and \( x_{n}=\sqrt{3 x_{n-1}} \) Show that \( \left(x_{n}\right) \) is

Consider the sequence defined as \( x_{1}=\sqrt{3} \) and \( x_{n}=\sqrt{3 x_{n-1}} \) Show that \( \left(x_{n}\right) \) is monotone increasing and bounded by 3 (Use induction)


We have an Answer from Expert

View Expert Answer

Expert Answer

Given, x1=3, xn=3xn?1, n?2 Here, xn>0, for all n? N Statement: (xn) is bounded
We have an Answer from Expert

Buy This Answer $5

Place Order

We Provide Services Across The Globe

Order Now
Go To Answered Questions