Create a simulation of the entire contents of the LDPC code through MATLAB based on the contents of the picture.
1. a theoretical explanation

2. Note 1. Example of results (This created based on code other than LDPC code)
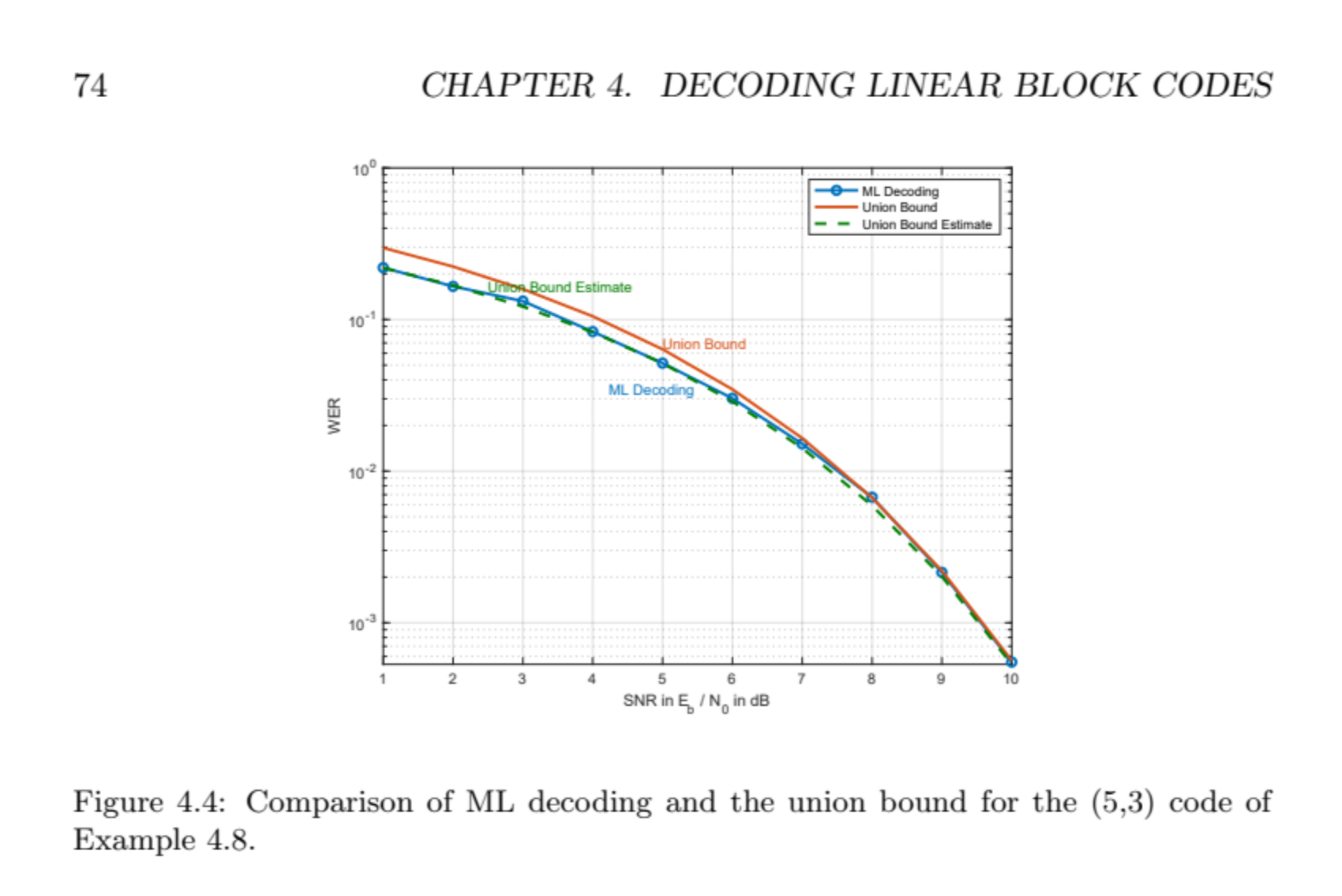
I need a graph as a result(x axis should be 1~10 like pic)
3. Note 2. Please refer to this

4. I asked before and got the following answer as a result, but this code doesn't provide a graph...



Based on this, please create a perfect LDPC simulation code like a graph picture
74 CHAPTER 4. DECODING LINEAR BLOCK CODES Figure 4.4: Comparison of ML decoding and the union bound for the (5,3) code of Example 4.8.
function syndromeDecodingExample (p, Nstop) G=[…? %Generator matrix ? 1?0?1?1?0?;?…? H=[0?1?0?1?1?]; \%Parity-check matrix 1?0?1?0?0?;?…? 1?1?0?1?0?;?…? 0?1?0?0?1?]; [k,n]=size(G); Phi =[…? %Syndrome decoder table ? 0?0?0?0?0?;?…? 0?0?1?0?0?;?…? 0?0?0?1?0?;?…? 1?0?0?0?0?;?…? 0?0?0?0?1?;?…? 0?0?1?0?1?;?…? 0?1?0?0?0?;?…? 0?1?1?0?0?]?] numberOfBitErrors =0; numberOfWordErrors =0; Nframes =0; while Nframes < Nstop \%encoder u=randi([0?1?],1,k); c=mod(u?G,2); \%channel e=rand(1,n)<p; y=mod(c+e,2); \%syndrome decoding s=mod(y?H?,2); ehat = Phi ( bi2de (s)+1,:);% binary - to-decimal conversion chat =mod(y? ehat, 2); nbe =sum(mod(c? chat, 2)); numberOfBitErrors = numberOfBitErrors + nbe; numberOfWordErrors = numberOfWordErrors +( nbe >0); Nframes = Nframes +1 ; end WER = numberOfWordErrors / Nframes; BER = numberOfBitErrors / (n * Nframes ); fprintf('Nerr =%d, WER =%G,BER=%G\n?, numberOfWordErrors, WER, BER) ; save decoding-data \%change filename to avoid overwrite \%another .m file loads and plots Figure 4.6: Matlab source code implementing simulation using syndrome decoding.
It seems that the provided text contains information related to decoding linear block codes using MATLAB, specifically focusing on syndrome decoding. Here is the general approach to simulating LDPC (Low-Density Parity-Check) codes in MATLAB Theoretical Explanation: LDPC codes are a class of error-correcting codes known for their excellent performance in terms of error correction. These codes are defined by sparse parity-check matrices, and their decoding often involves iterative algorithms. In the context of syndrome decoding, the idea is to use the syndrome (the result of the modulo2 sum of received bits and the parity-check matrix) to identify and correct errors in the received codeword. General Approach to SimulatingLDPC Codes in MATLAB: 1. Define LDPC Code Parameters: - Parity-check matrix H: A sparse matrix defining the code. - Codeword length n and message length k. 2. Generate Random Message: - Generate a random binary message of length k. 3. Encode the Message: - Use the parity-check matrix H to encode the message into a codeword. 4. AddNoise : - Simulate a communication channel by adding noise to the codeword. 5. Decode Using Syndrome Decoding: - Compute the syndrome by taking the modulo-2 sum of the received bits and the transpose of the parity-check matrix H?. - Create a syndrome decoding table (?) to map syndromes to error patterns. - Estimate the error pattern (e?) based on the syndrome. - Correct the received codeword by subtracting the estimated error pattern. 6. Evaluate Performance Metrics: - Calculate the number of bit errors, word errors, and relevant performance metrics such as Word Error Rate (WER) and Bit Error Rate (BER). 7. Repeat for Multiple Frames: - Repeat the process for a specified number of frames to obtain statistical measures. Explanation: In this step the theoretical approach and the General Approach to SimulatingLDPC Codes in MATLAB is explained in this step.
MATLAB Code Structure: The provided image shows an example MATLAB code for simulating an LDPC code using syndrome decoding. The code defines the generator matrix, parity-check matrix, and syndrome decoder table. It then iterates through multiple frames, performing encoding, channel modeling, syndrome decoding, and error counting. Finally, it calculates and displays the WER and BER. However, to simulate the specific LDPC code in the image, you would need the following information: - Generator matrix (G): This defines the relationship between the data bits and the codewords. - Parity-check matrix (H): This specifies the parity constraints that the codewords must satisfy. - Channel model: This defines the type and amount of noise introduced during transmission. - Decoding algorithm: You can choose different decoding algorithms like belief propagation or min-sum depending on the code and desired performance. MATLAB Code for LDPC Code Simulation
\& Def ine the generator matrix (G) and parity-check matrix (H) G=[ 10110; 01011; 11010; 01001; 10100; ]; H=[ 01011; 10100; 11010; 01001 ; ]; y Set other parameters Nstop = 1000; 8 Number of frames to simulate p=0.05; : Channel bit error probability k=size(G,2); Number of information bits n=size(G,1);x Number of codeword bits 8 Initialize error counters numberDfBitErrors =0; number[f WordErrors = 0; 8 Simulation loop for i=1 : Nstop \& Generate random information bits u=randi([0?1?],1,k); 8 Encode information bits to codeword c=mod(u+G,2); 8 Simulate channel errors e=rand(1,n)<p; y=mod(c+e,2); 8 Syndrome decoding s=mod(y+H?,2); ehat = Phi (bi2de (s)+1,:); 8 Correct errors and calculate errors chat =mod(y? ehat, 2); nbe =sum(mod(c? chat, 2)); numberDfBitErrors = numberDfBitErrors + nbe: numberDf WordErrors = numberDf WordErrors +( nbe >0); end \& Calculate and display performance metrics WER = numberDf WordErrors / Nstop; BER= numberDfBitErrors /(k+ Nstop ); fprintf ('Word Error Rate (WER): \&gW?', WER); fprintf('Bit Error Rate (BER): 'sg"In', BER): Explanation: In this step the theory and the MATLAB code for the LDPC simulation is explained.
Explanation of the code: 1. The code defines the generator matrix (G) and parity-check matrix (H) specific to the LDPC code in the image. 2. It sets other simulation parameters like number of frames, channel error probability, information bits, and codeword bits. 3. Error counters are initialized for tracking bit and word errors. 4. The loop iterates for Nstop frames: - Random information bits are generated. - The codeword is obtained by multiplying the information bits with the generator matrix and taking the modulo 2 residue. - Channel errors are simulated by generating random bit errors with probability p. - Syndrome decoding is performed by multiplying the received vector with the transpose of the parity-check matrix and taking the modulo 2 residue. - The syndrome decoder table (Phi) is used to estimate the error pattern based on the syndrome. - Errors are corrected in the received vector to obtain the estimated codeword. - Number of bit errors and word errors are calculated based on the original and estimated codewords. 5. Finally, the WER and BERare calculated and displayed. Note: This is a basic example of LDPC code simulation. You can modify the code to incorporate different channel models, decoding algorithms, and performance metrics as needed for your specific research or application. Explanation: The explanation for the Matlab code is provided in this step






