(Solved): Data shown below is expected to obey the power law; \[ y=A x^{n} \] For the data given below, plot ...

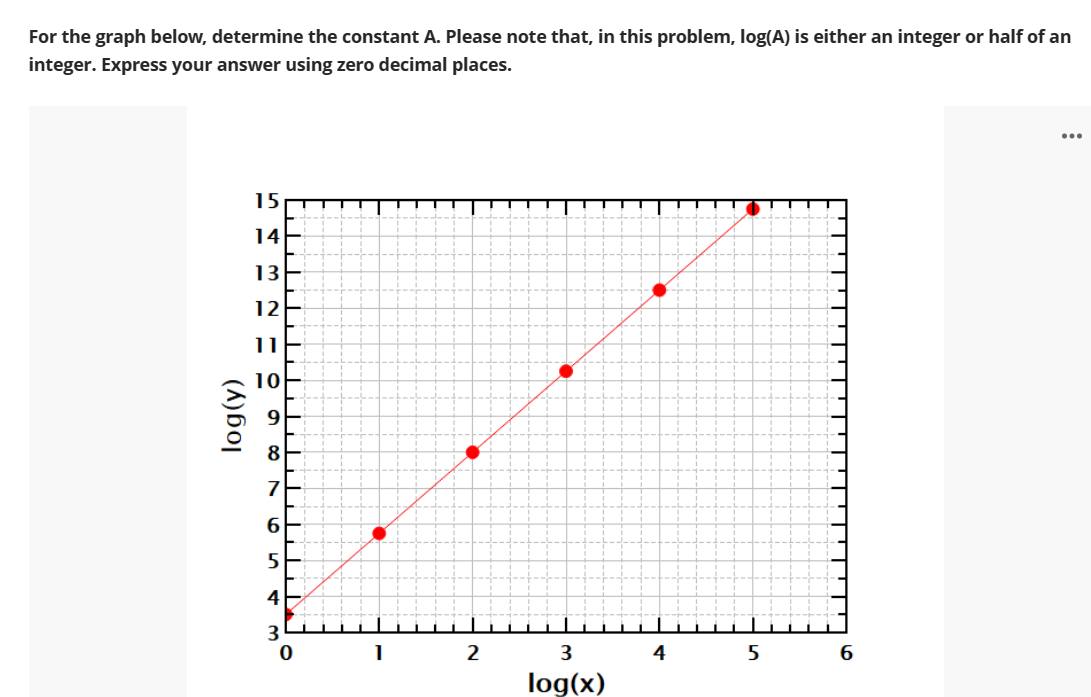
Data shown below is expected to obey the power law; \[ y=A x^{n} \] For the data given below, plot a \( \log (y) \) vs. \( \log (x) \) graph (either using a computer or by hand), and after doing a linear fit (drawing the best fit line), determine the constant \( A \). Express your answer using zero decimal places. In many branches of science and engineering a common equation, relating two physical quantities, we might encounter is of the form: \[ y=A x^{n} \] where \( A \) is a constant. If one would like to confirm a power law and figure out what \( A \) and \( n \) are, one way to do that is to plot a loglog graph of \( y \) and \( x \). 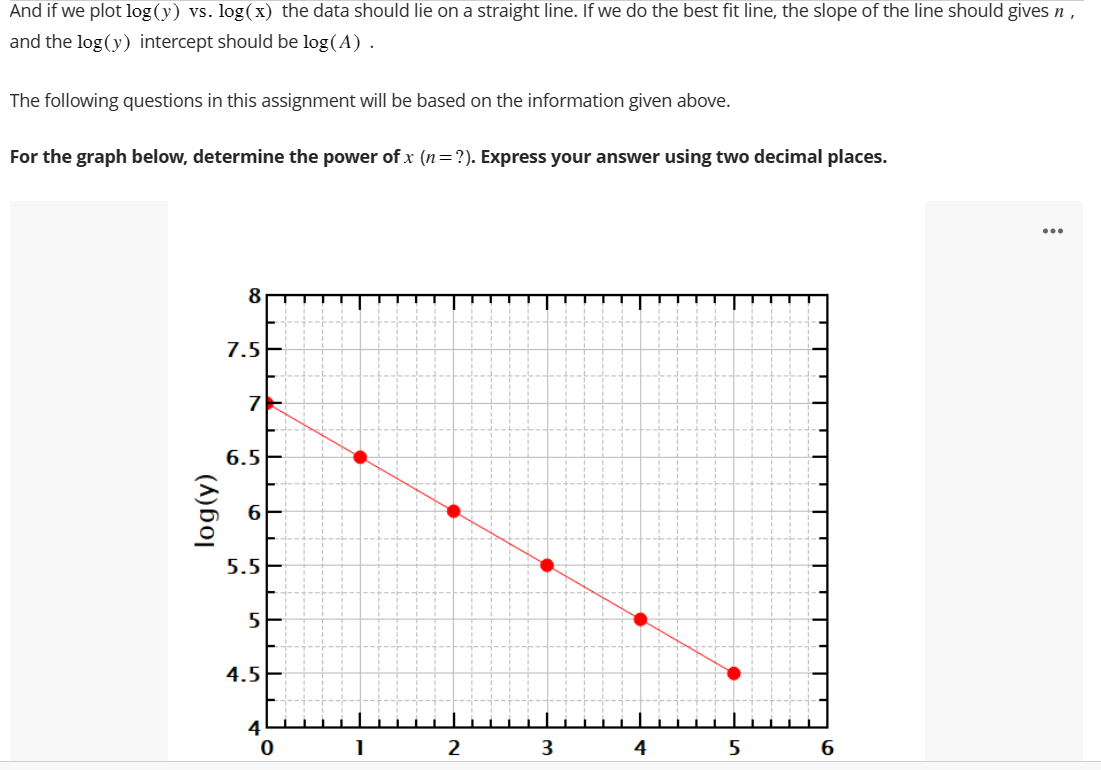If one takes the logarithm of both sides, one obtains: \[ \log (y)=\log \left(A x^{n}\right) \] and since we know that \[ \log (a b)=\log (a)+\log (b) \] and \( \log \left(c^{d}\right)=d \log (c) \) we get: \[ \log (y)=\log (A)+n \log (x) \] And if we plot \( \log (y) \) vs. \( \log (\mathrm{x}) \) the data should lie on a straight line. If we do the best fit line, the slope of the line should gives \( n \), and the \( \log (y) \) intercept should be \( \log (A) \). The following questions in this assignment will be based on the information given above. For the graph below, determine the power of \( x(n=?) \). Express your answer using two decimal places. In many branches of science and engineering a common equation, relating two physical quantities, we might encounter is of the form: \[ y=A x^{n} \] where \( A \) is a constant. If one would like to confirm a power law and figure out what \( A \) and \( n \) are, one way to do that is to plot a loglog graph of \( y \) and \( x \). If one takes the logarithm of both sides, one obtains: \[ \log (y)=\log \left(A x^{n}\right) \] and since we know that \[ \log (a b)=\log (a)+\log (b) \] and \[ \log \left(c^{d}\right)=d \log (c) \] we get: \[ \log (y)=\log (A)+n \log (x) \] And if we plot \( \log (y) \) vs. \( \log (\mathrm{x}) \) the data should lie on a straight line. If we do the best fit line, the slope of the line should gives \( n \), and the \( \log (y) \) intercept should be \( \log (A) \). The following questions in this assignment will be based on the information given above. For the graph below, determine the constant A. Please note that, in this problem, \( \log (\mathrm{A}) \) is either an integer or half of an integer. Express your answer using zero decimal places. In many branches of science and engineering a common equation, relating two physical quantities, we might encounter is of the form: \[ y=A x^{n} \] where \( A \) is a constant. If one would like to confirm a power law and figure out what \( A \) and \( n \) are, one way to do that is to plot a log\( \log \) graph of \( y \) and \( x \). If one takes the logarithm of both sides, one obtains: \[ \log (y)=\log \left(A x^{n}\right) \] and since we know that \[ \log (a b)=\log (a)+\log (b) \] and \( \log \left(c^{d}\right)=d \log (c) \) we get: \[ \log (y)=\log (A)+n \log (x) \] And if we plot \( \log (y) \) vs. \( \log (\mathrm{x}) \) the data should lie on a straight line. If we do the best fit line, the slope of the line should gives \( n \), and the \( \log (y) \) intercept should be \( \log (A) \). The following questions in this assignment will be based on the information given above. For a given data set, the slope of the best fit line to the log-log graph is given to be 1.26. What is the power \( x \) ? Express your In many branches of science and engineering a common equation, relating two physical quantities, we might encounter is of the form: \[ y=A x^{n} \] where \( A \) is a constant. If one would like to confirm a power law and figure out what \( A \) and \( n \) are, one way to do that is to plot a loglog graph of \( y \) and \( x \). If one takes the logarithm of both sides, one obtains: \[ \log (y)=\log \left(A x^{n}\right) \] and since we know that \( \log (a b)=\log (a)+\log (b) \) and \( \log \left(c^{d}\right)=d \log (c) \) we get: \[ \log (y)=\log (A)+n \log (x) \] And if we plot \( \log (y) \) vs. \( \log (x) \) the data should lie on a straight line. If we do the best fit line, the slope of the line should gives \( n \), and the \( \log (y) \) intercept should be \( \log (A) \). The following questions in this assignment will be based on the information given above. For a given data set, the best fit line to the log-log graph lies on a line and the \( y \)-intercept of the line is found to be \( 0.35 \). Determine the value of A. Express vour answer using one decimal place.