(Solved): Design for \( \mathbf{Z} \) K-map for Z Simplest SOP \( = \) Simplest POS \( = \) Realization and ...

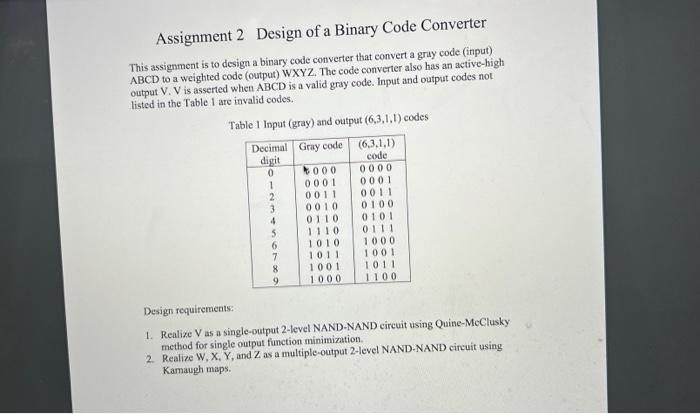
Design for \( \mathbf{Z} \) K-map for Z Simplest SOP \( = \) Simplest POS \( = \) Realization and gate transformation for \( Z \) Draw the circuit for \( \mathrm{Z} \) with only NAND gates. Assignment 2 Design of a Binary Code Converter This assignment is to design a binary code converter that convert a grisy code (input) ABCD to a weighted code (output) WXYZ. The code converter also has an active-high output V. V is asserted whet ABCD is a valid gray code. Input and output codes not listed in the Table I are invalid codes. Table 1 Input (gray) and output \( (6,3,1,1) \) codes Design requirements: 1. Realize \( \mathrm{V} \) as a single-output 2-level NAND-NAND circuit using Quine-MeClusky method for single output function minimization. 2. Realizo \( \mathrm{W}, \mathrm{X}, \mathrm{Y} \), and \( \mathrm{Z} \) as a multiple-output 2-level NAND-NAND circuit using Kamaugh maps. 1. Input and output code assignment Input gray code: Gray Code Output weighted code: 2. Formulation of code converter Truth table for code converter (If \( \mathrm{ABCD} \) is an invalid Express \( \mathrm{V}, \mathrm{W}, \mathrm{X}, \mathrm{Y}, \mathrm{Z} \) in minterm list form \[ \begin{array}{l} V=\Sigma m( \\ W=\Sigma m( \\ X=\Sigma m( \\ Y=\Sigma m( \\ Z=\Sigma m( \end{array} \]