(Solved): Determine if the following piecewise defined function is differentiable at \( x=0 \). \[ f(x)=\left ...

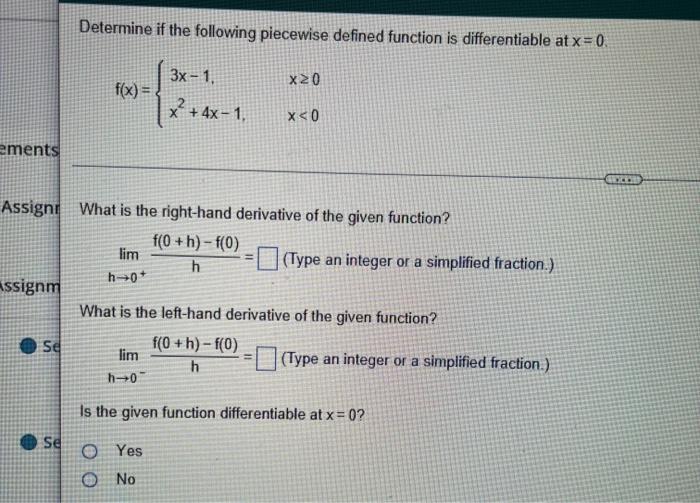
Determine if the following piecewise defined function is differentiable at \( x=0 \). \[ f(x)=\left\{\begin{array}{ll} 3 x-1, & x \geq 0 \\ x^{2}+4 x-1, & x<0 \end{array}\right. \] What is the right-hand derivative of the given function? \( \lim _{h \rightarrow 0^{+}} \frac{f(0+h)-f(0)}{h}=\quad \) (Type an integer or a simplified fraction.) What is the left-hand derivative of the given function? \[ \lim _{h \rightarrow 0^{-}} \frac{f(0+h)-f(0)}{h}=\text { (Type an integer or a simplified fraction.) } \] Is the given function differentiable at \( x=0 \) ? Yes No Find the first and second derivatives. 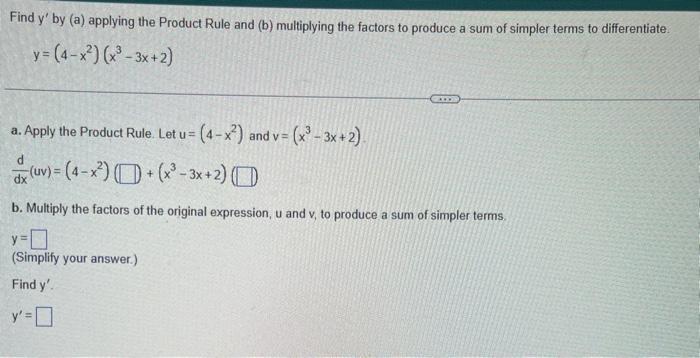\[ s=6 t^{5}-5 t^{6} \] \[ \frac{d s}{d t}= \] \[ \frac{d^{2} s}{d t^{2}}= \] Find \( y^{\prime} \) by (a) applying the Product Rule and (b) multiplying the factors to produce a sum of simpler terms to differentiate. \[ y=\left(4-x^{2}\right)\left(x^{3}-3 x+2\right) \] a. Apply the Product Rule. Let \( u=\left(4-x^{2}\right) \) and \( v=\left(x^{3}-3 x+2\right) \) \[ \frac{d}{d x}(u v)=\left(4-x^{2}\right) \quad 1+\left(x^{3}-3 x+2\right) \] b. Multiply the factors of the original expression, \( u \) and \( v \), to produce a sum of simpler terms. \[ y= \] (Simplify your answer.) Find \( y^{\prime} \). \[ y^{\prime}= \]