Home /
Expert Answers /
Computer Science /
equivalent-transformations-use-a-chain-of-equivalences-to-transform-the-sentence-not-ab-gt-bv-pa686
(Solved): Equivalent transformations Use a chain of equivalences to transform the sentence not((AB)->(Bv ...
Equivalent transformations
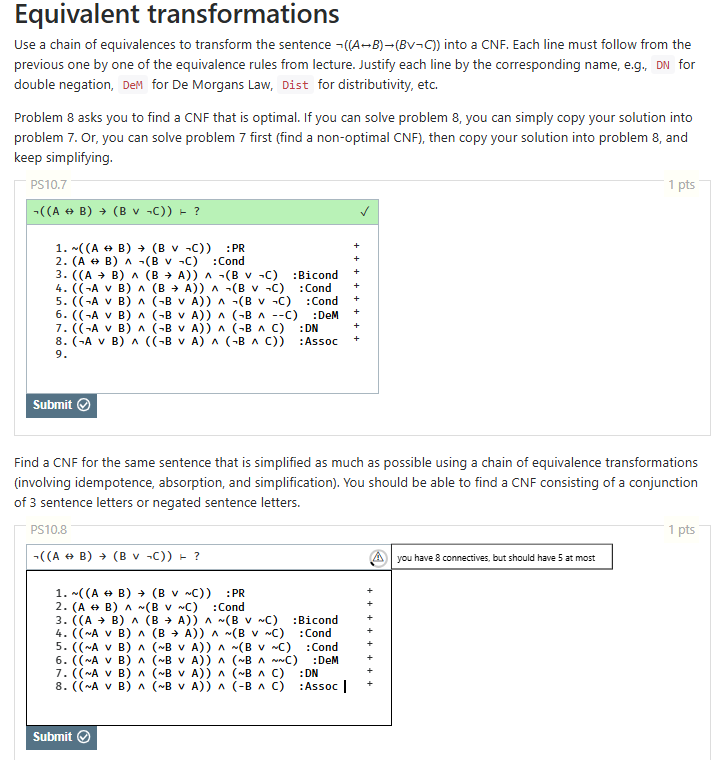
Use a chain of equivalences to transform the sentence not((A?B)->(BvvnotC)) into a CNF. Each line must follow from the
previous one by one of the equivalence rules from lecture. Justify each line by the corresponding name, e.g., DN for
double negation, DeM for De Morgans Law, Dist for distributivity, etc.
Problem 8 asks you to find a CNF that is optimal. If you can solve problem 8 , you can simply copy your solution into
problem 7. Or, you can solve problem 7 first (find a non-optimal CNF), then copy your solution into problem 8, and
keep simplifying.
PS10.7
not((A<=>B)->(BvvnotC))|--?
?((AharrB)->(BvvnotC)):PR
(AharrB)^(^())not(BvvnotC) :Cond
((A->B)^(^())(B->A))^(^())not(BvvnotC) :Bicond +
((notAvvB)^(^())(B->A))^(^())not(BvvnotC) :Cond +
((notAvvB)^(^())(notBvvA))^(^())not(BvvnotC) :Cond +
((notAvvB)^(^())(notBvvA))^(^())(notB^(^())--C):DeM+
((notAvvB)^(^())(notBvvA))^(^())(notB^(^())C):DN+
(notAvvB)^(^())((notBvvA)^(^())(notB^(^())C)): Assoc +
Find a CNF for the same sentence that is simplified as much as possible using a chain of equivalence transformations
(involving idempotence, absorption, and simplification). You should be able to find a CNF consisting of a conjunction
of 3 sentence letters or negated sentence letters.
PS10.8?
please answer 10.8!