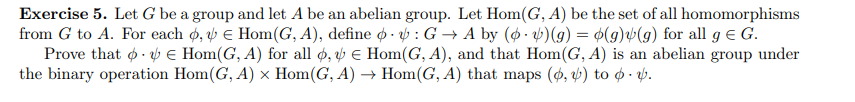(Solved): Exercise 5. Let G be a group and let A be an abelian group. Let Hom(G, A) be the set of all homomo ...

Exercise 5. Let G be a group and let A be an abelian group. Let Hom(G, A) be the set of all homomorphisms from G to A. For each o, & Hom(G, A), define : G?A by (o)(g) = (g)(g) for all g € G. Prove that e Hom(G, A) for all o, & Hom(G, A), and that Hom(G, A) is an abelian group under the binary operation Hom(G, A) × Hom(G, A) ? Hom(G, A) that maps (o,) to .