(Solved): Figure 4: Cluster Data for Various Sports Review the table labeled Figure 4: Cluster Data for Vari ...

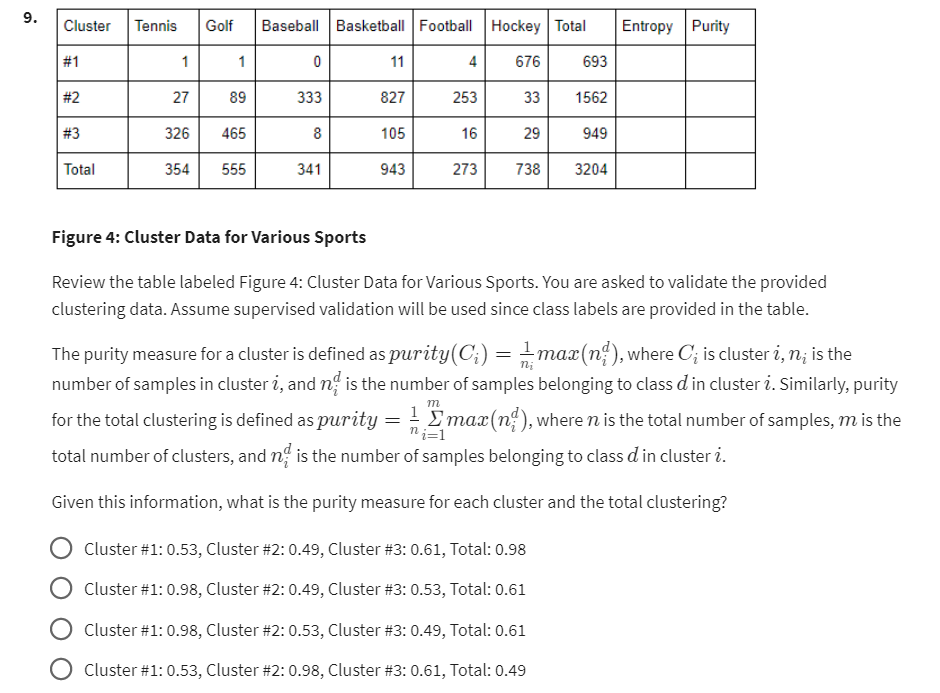
Figure 4: Cluster Data for Various Sports Review the table labeled Figure 4: Cluster Data for Various Sports. You are asked to validate the provided clustering data. Assume supervised validation will be used since class labels are provided in the table. The purity measure for a cluster is defined as purity \( \left(C_{i}\right)=\frac{1}{n_{i}} \max \left(n_{i}^{d}\right) \), where \( C_{i} \) is cluster \( i, n_{i} \) is the number of samples in cluster \( i \), and \( n_{i}^{d} \) is the number of samples belonging to class \( d \) in cluster \( i \). Similarly, purity for the total clustering is defined as purity \( =\frac{1}{n} \sum_{i=1}^{m} \max \left(n_{i}^{d}\right) \), where \( n \) is the total number of samples, \( m \) is the total number of clusters, and \( n_{i}^{d} \) is the number of samples belonging to class \( d \) in cluster \( i \). Given this information, what is the purity measure for each cluster and the total clustering? Cluster #1: \( 0.53 \), Cluster #2: \( 0.49 \), Cluster #3: \( 0.61 \), Total: \( 0.98 \) Cluster #1: \( 0.98 \), Cluster #2: \( 0.49 \), Cluster #3: \( 0.53 \), Total: \( 0.61 \) Cluster #1: \( 0.98 \), Cluster #2: \( 0.53 \), Cluster #3: \( 0.49 \), Total: \( 0.61 \) Cluster #1: \( 0.53 \), Cluster #2: \( 0.98 \), Cluster #3: \( 0.61 \), Total: \( 0.49 \)