(Solved): Figure 5. Frequency multiplexing modulation/demodulation system Consider the ...

???????

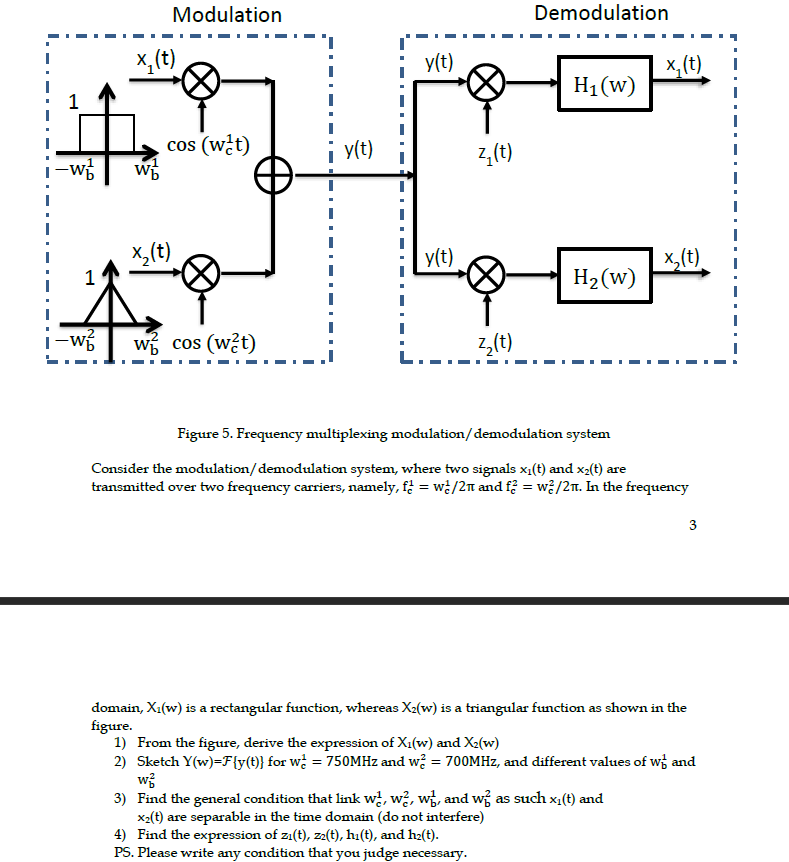
Figure 5. Frequency multiplexing modulation/demodulation system Consider the modulation/demodulation system, where two signals \( x_{1}(t) \) and \( x_{2}(t) \) are transmitted over two frequency carriers, namely, \( f_{c}^{1}=w_{c}^{1} / 2 \pi \) and \( f_{c}^{2}=w_{c}^{2} / 2 \pi \). In the frequency 3 domain, \( \mathrm{X}_{1}(w) \) is a rectangular function, whereas \( X_{2}(w) \) is a triangular function as shown in the figure. 1) From the figure, derive the expression of \( X_{1}(w) \) and \( X_{2}(w) \) 2) Sketch \( Y(w)=\mathcal{F}\{y(t)\} \) for \( w_{c}^{1}=750 \mathrm{MHz} \) and \( w_{c}^{2}=700 \mathrm{MHz} \), and different values of \( w_{b}^{1} \) and \( w_{b}^{2} \) 3) Find the general condition that link \( w_{\mathrm{c}}^{1}, w_{\mathrm{c}}^{2}, w_{b^{\prime}}^{1} \), and \( w_{b}^{2} \) as such \( x_{1}(t) \) and \( \mathrm{x}_{2}(\mathrm{t}) \) are separable in the time domain (do not interfere) 4) Find the expression of \( z_{1}(t) \), \( z_{2}(t), h_{1}(t) \), and \( h_{2}(t) \). PS. Please write any condition that you judge necessary.