Home /
Expert Answers /
Computer Science /
find-the-shortest-paths-between-all-pairs-of-vertices-in-the-graph-below-usin-pa119
Expert Answer
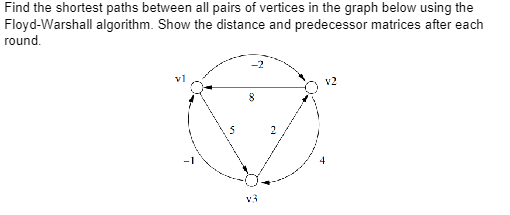
GIVEN: The question asks us to find the shortest paths between all pairs of vertices in a graph using the Floyd-Warshall algorithm.The graph has three vertices labeled v1, v2, and v3, and the distance between pairs of vertices is provided.The distance from v1 to v2 is -2, the distance from v2 to v3 is 4, and the distance from v3 to v1 is -1. We are asked to apply the Floyd-Warshall algorithm to find the shortest path distances between all pairs of vertices and show the distance and predecessor matrices after each round. The algorithm will give us the shortest path distances between all pairs of vertices in the graph, allowing us to determine the shortest path between any two vertices in the graph The Floyd-Warshall algorithm is a dynamic programming algorithm used to find the shortest path between all pairs of vertices in a directed, weighted graph. The algorithm works by considering all possible intermediate vertices between any two vertices in the graph and updating the distances accordingly. The time complexity of the algorithm is O(n^3), where n is the number of vertices in the graph. Above the explanation is algorithm will give us the shortest path distances between all pairs of vertices in the graph, allowing us to determine the shortest path between any two vertices in the graph.
 ???????
???????