(Solved): If \( \mathrm{n}=14, \bar{x}(\mathrm{x}-\mathrm{bar})=50 \), and \( \mathrm{s}=6 \), find the margi ...

If \( \mathrm{n}=14, \bar{x}(\mathrm{x}-\mathrm{bar})=50 \), and \( \mathrm{s}=6 \), find the margin of error at a \( 90 \% \) confidence level Give your answer to two decimal places. In a survey, 30 people were asked how much they spent on their child's last birthday gift. The results were roughly bell-shaped with a mean of \( \$ 33 \) and standard deviation of \( \$ 6 \). Find the margin of error at a \( 95 \% \) confidence level. Give your answer to two decimal places. 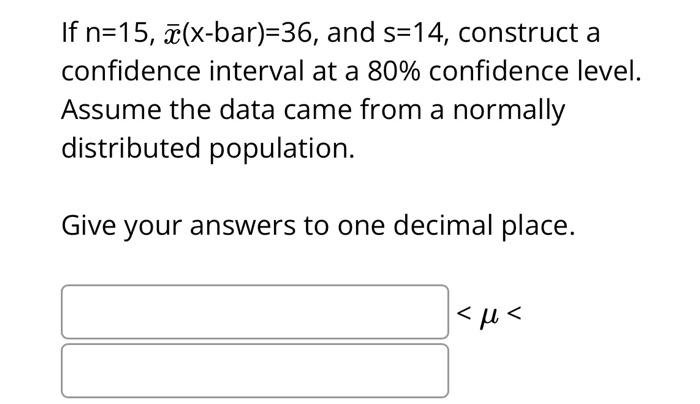If \( \mathrm{n}=15, \bar{x}(\mathrm{x}-\mathrm{bar})=36 \), and \( \mathrm{s}=14 \), construct a confidence interval at a \( 80 \% \) confidence level. Assume the data came from a normally distributed population. Give your answers to one decimal place. \[ \mid<\mu< \] In a survey, 12 people were asked how much they spent on their child's last birthday gift. The results were roughly bell-shaped with a mean of \( \$ 33 \) and sample standard deviation of \( \$ 19 \). Construct a confidence interval at a \( 98 \% \) confidence level. Give your answers to one decimal place. \[ <\mu< \] Karen wants to advertise how many chocolate chips are in each Big Chip cookie at her bakery. She randomly selects a sample of 51 cookies and finds that the number of chocolate chips per cookie in the sample has a mean of \( 17.8 \) and a standard deviation of 2.6. What is the \( 98 \% \) confidence interval for the number of chocolate chips per cookie for Big Chip cookies? Enter your answers accurate to one decimal place. \[ <\mu< \]