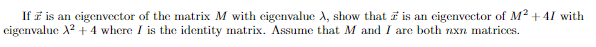(Solved): If \( \vec{x} \) is an eigenvector of the matrix \( M \) with eigenvalue \( \lambda \), show that ...

If \( \vec{x} \) is an eigenvector of the matrix \( M \) with eigenvalue \( \lambda \), show that \( \vec{x} \) is an eigenvector of \( M^{2}+4 I \) with eigenvalue \( \lambda^{2}+4 \) where \( I \) is the identity matrix. \( \Lambda \) ssume that \( M \) and \( I \) are both \( n \times n \) matrices.