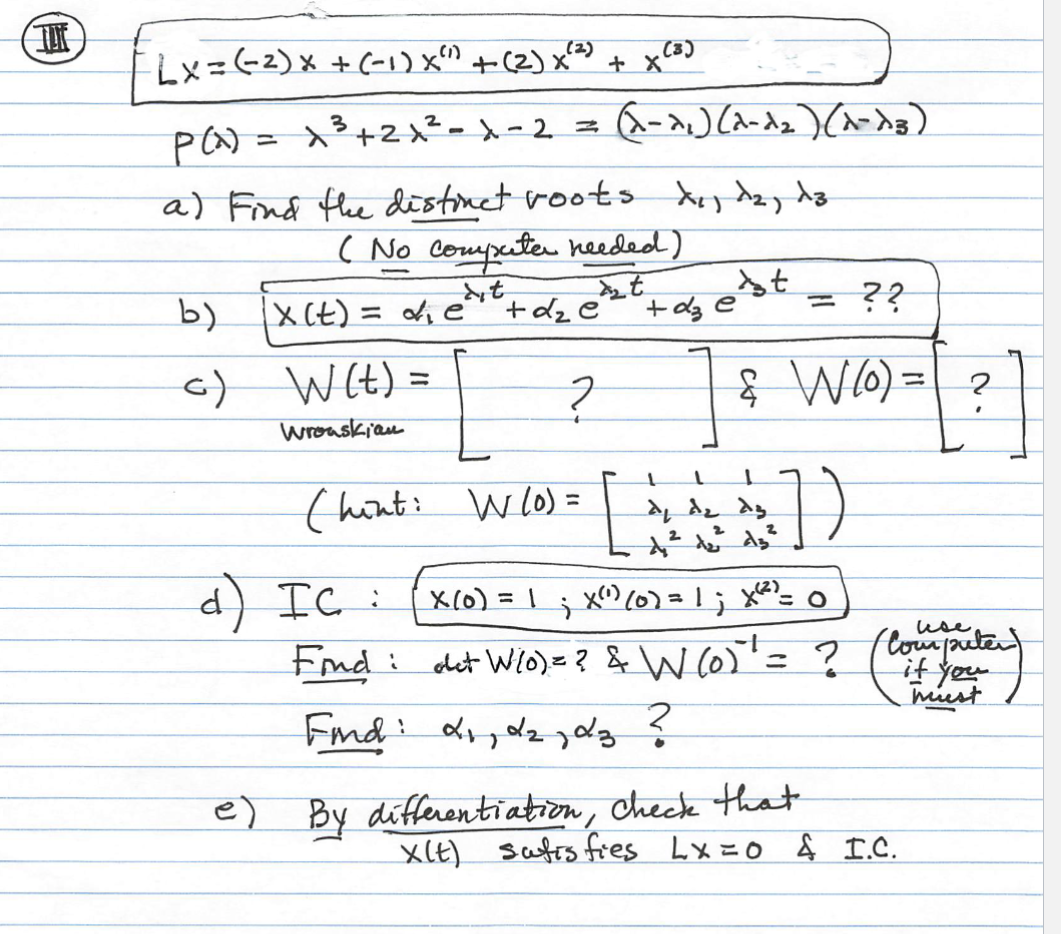Home /
Expert Answers /
Advanced Math /
iiii-lx-2-x-1-x-1-2-x-2-x-3-p-lambda-lambda-3-2-lambda-2-lambda-2-gt-pa700
(Solved): (IIII) Lx=(-2)x+(-1)x^((1))+(2)x^((2))+x^((3)) P(\lambda )=\lambda ^(3)+2\lambda ^(2)-\lambda -2=> ...
(IIII)
Lx=(-2)x+(-1)x^((1))+(2)x^((2))+x^((3))
P(\lambda )=\lambda ^(3)+2\lambda ^(2)-\lambda -2=>(\lambda -\lambda _(1))(\lambda -\lambda _(2))(\lambda -\lambda _(3))
a\lambda _(1),\lambda _(2),\lambda _(3)
(No compcuter reeded)
bx(t)=\alpha _(1)e^(\lambda _(1)t)+\alpha _(2)e^(\lambda _(2)t)+\alpha _(3)e^(\lambda _(3)t)= ??
cW(0)=[[1,1,1],[\lambda _(1),\lambda _(2),\lambda _(3)],[\lambda _(1)^(2),\lambda _(2)^(2),\lambda _(3)^(2)]] x(0)=1;x^((1))(0)=1;x^((2))=0
Find: detW(0)= ? & W(0)^(-1)= ? ([ cousputer ],[ if your ],[ nuest ])
Find: \alpha _(1),\alpha _(2),\alpha _(3) ?
ex(t) sutisfies Lx=0& I.C.