(Solved): In a combined gas turbine-steam power plant, the topping cycle is a simple Brayton cycle that has ...

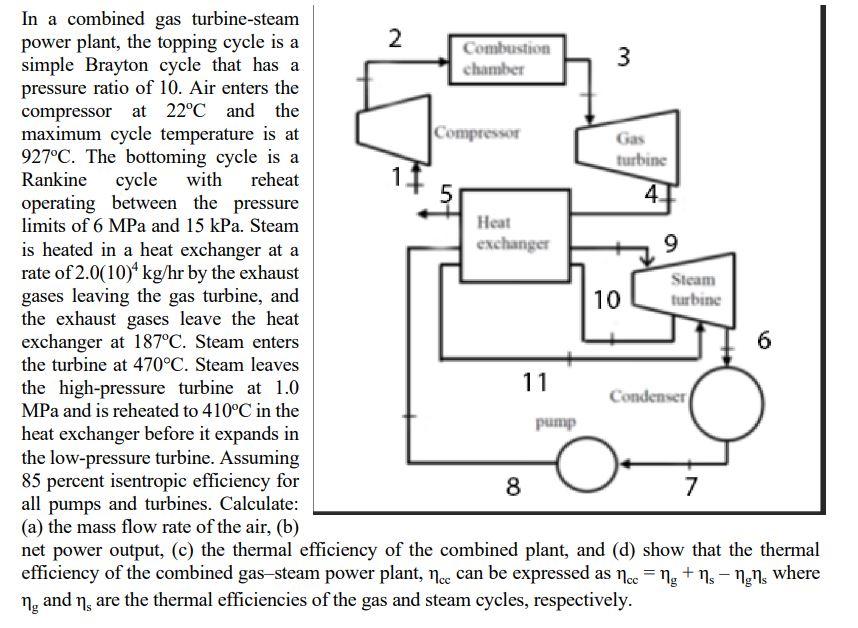
In a combined gas turbine-steam power plant, the topping cycle is a simple Brayton cycle that has a pressure ratio of 10 . Air enters the compressor at \( 22^{\circ} \mathrm{C} \) and the maximum cycle temperature is at \( 927^{\circ} \mathrm{C} \). The bottoming cycle is a Rankine cycle with reheat operating between the pressure operating between the pressure limits of \( 6 \mathrm{MPa} \) and \( 15 \mathrm{kPa} \). Steam is heated in a heat exchanger at a rate of \( 2.0(10)^{4} \mathrm{~kg} / \mathrm{hr} \) by the exhaust gases leaving the gas turbine, and the exhaust gases leave the heat exchanger at \( 187^{\circ} \mathrm{C} \). Steam enters the turbine at \( 470^{\circ} \mathrm{C} \). Steam leaves the high-pressure turbine at \( 1.0 \) the high-pressure turbine at \( 1.0 \) \( \mathrm{MPa} \) and is reheated to \( 410^{\circ} \mathrm{C} \) in the heat exchanger before it expands in the low-pressure turbine. Assuming 85 percent isentropic efficiency for all pumps and turbines. Calculate: (a) the mass flow rate of the air, (b) net power output, (c) the thermal efficiency of the combined plant, and (d) show that the thermal efficiency of the combined gas-steam power plant, \( \eta_{\mathrm{cc}} \) can be expressed as \( \eta_{\mathrm{cc}}=\eta_{\mathrm{g}}+\eta_{\mathrm{s}}-\eta_{\mathrm{g}} \eta_{\mathrm{s}} \) where \( \eta_{\mathrm{g}} \) and \( \eta_{\mathrm{s}} \) are the thermal efficiencies of the gas and steam cycles, respectively.