(Solved): In a simple linear regression based on 30 observations, it is found that \( b_{1}=3.25 \) and \( s ...

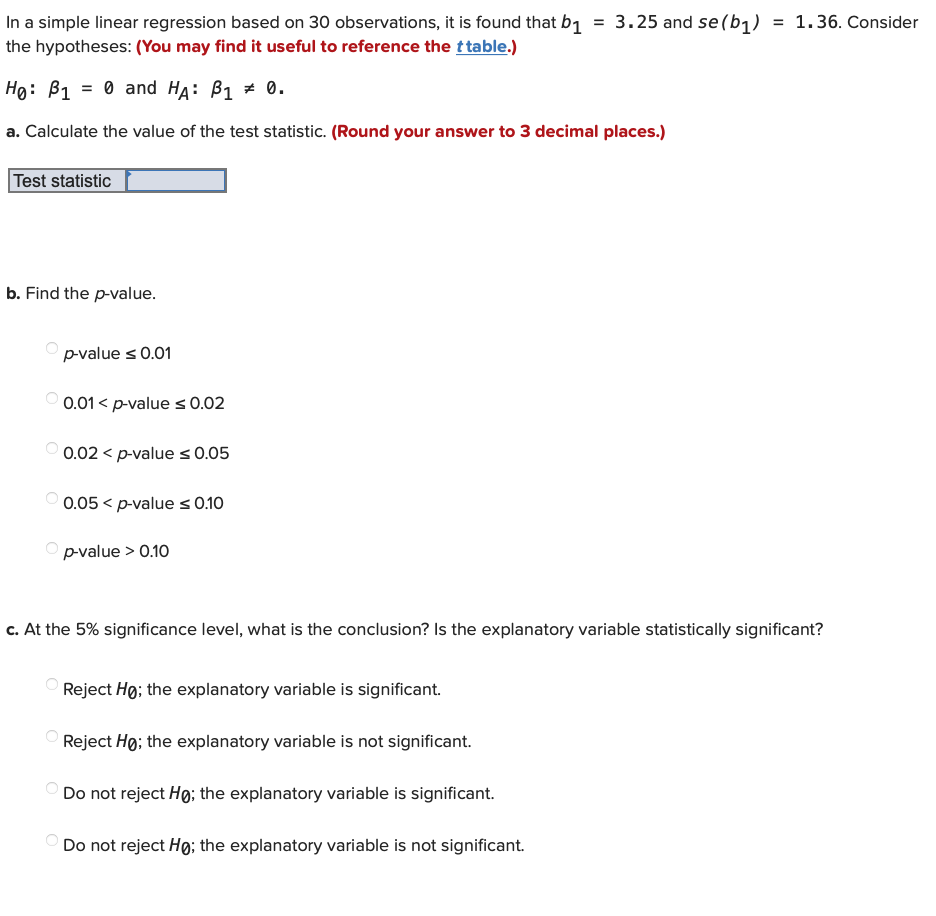
In a simple linear regression based on 30 observations, it is found that \( b_{1}=3.25 \) and \( s e\left(b_{1}\right)=1.36 \). Consider the hypotheses: (You may find it useful to reference the \( \underline{t} \) table.) \( H_{0}: \beta_{1}=0 \) and \( H_{A}: \beta_{1} \neq 0 \). a. Calculate the value of the test statistic. (Round your answer to 3 decimal places.) b. Find the \( p \)-value. \[ \begin{array}{l} p \text {-value } \leq 0.01 \\ 0.01

0.10 \end{array} \] c. At the \( 5 \% \) significance level, what is the conclusion? Is the explanatory variable statistically significant? Reject \( \mathrm{HO}_{0} \); the explanatory variable is significant. Reject \( \mathrm{Hg}_{0} \); the explanatory variable is not significant. Do not reject \( H_{0} \); the explanatory variable is significant. Do not reject \( \mathrm{H}_{0} \); the explanatory variable is not significant.