(Solved): In the AC circuit shown, the component values are chosen such that \( R_{1}=20 \Omega \); \( R_{2}= ...

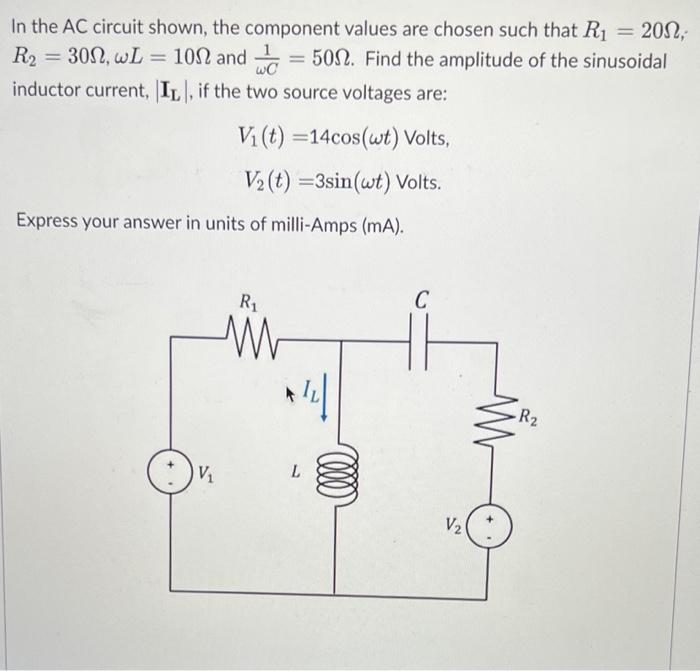
In the AC circuit shown, the component values are chosen such that \( R_{1}=20 \Omega \); \( R_{2}=30 \Omega, \omega L=10 \Omega \) and \( \frac{1}{\omega C}=50 \Omega \). Find the amplitude of the sinusoidal inductor current, \( \left|\mathbf{I}_{\mathrm{L}}\right| \), if the two source voltages are: \[ \begin{array}{c} V_{1}(t)=14 \cos (\omega t) \text { Volts, } \\ V_{2}(t)=3 \sin (\omega t) \text { Volts. } \end{array} \] Express your answer in units of milli-Amps (mA).