(Solved): Interference of Ultrasonic waves Suppose you are helping a researcher develop a method to use ultra ...

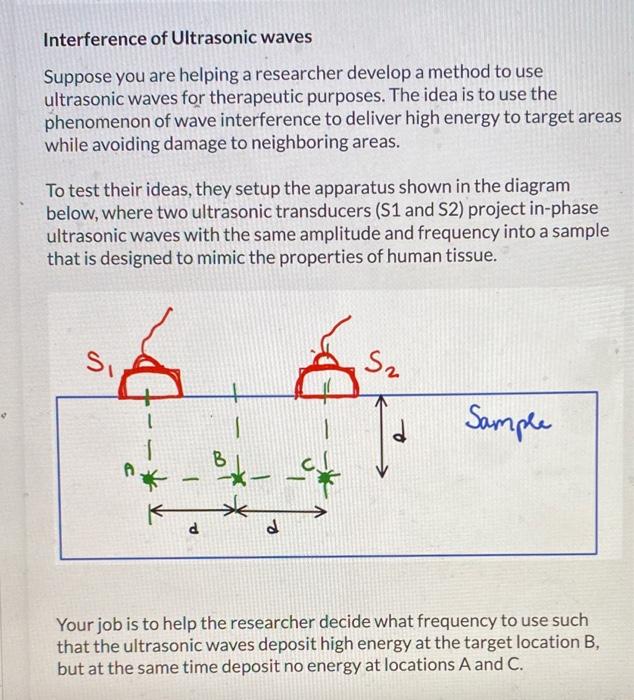
Interference of Ultrasonic waves Suppose you are helping a researcher develop a method to use ultrasonic waves for therapeutic purposes. The idea is to use the phenomenon of wave interference to deliver high energy to target areas while avoiding damage to neighboring areas. To test their ideas, they setup the apparatus shown in the diagram below, where two ultrasonic transducers (S1 and S2) project in-phase ultrasonic waves with the same amplitude and frequency into a sample that is designed to mimic the properties of human tissue. Your job is to help the researcher decide what frequency to use such that the ultrasonic waves deposit high energy at the target location \( B \), but at the same time deposit no energy at locations \( A \) and \( C \). 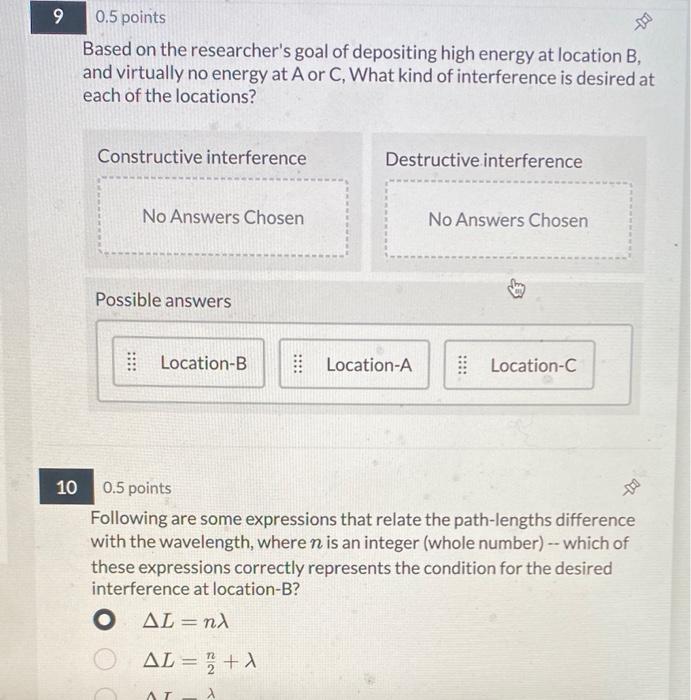Based on the researcher's goal of depositing high energy at location B, and virtually no energy at \( A \) or \( C \), What kind of interference is desired at each of the locations? Constructive interference Destructive interference Possible answers (m) \( 0.5 \) points Following are some expressions that relate the path-lengths difference with the wavelength, where \( n \) is an integer (whole number) - which of these expressions correctly represents the condition for the desired interference at location-B? 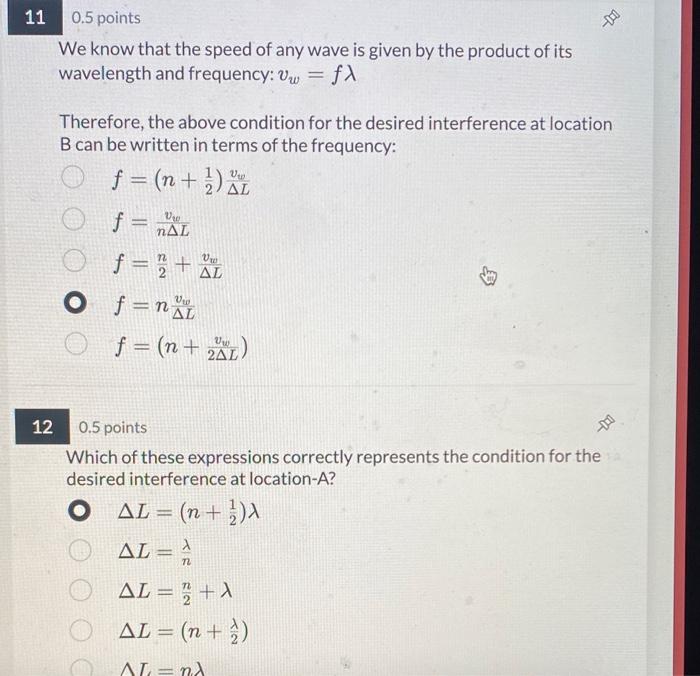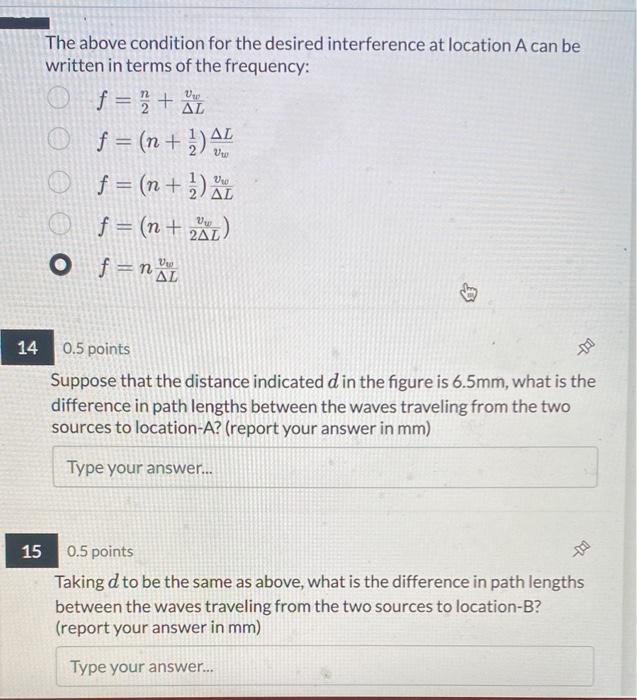\[ \begin{array}{l} \Delta L=n \lambda \\ \Delta L=\frac{n}{2}+\lambda \end{array} \] We know that the speed of any wave is given by the product of its wavelength and frequency: \( v_{w}=f \lambda \) Therefore, the above condition for the desired interference at location \( B \) can be written in terms of the frequency: \[ \begin{array}{l} f=\left(n+\frac{1}{2}\right) \frac{v_{w}}{\Delta L} \\ f=\frac{v_{w}}{n \Delta L} \\ f=\frac{n}{2}+\frac{v_{w}}{\Delta L} \\ f=n \frac{v_{w}}{\Delta L} \\ f=\left(n+\frac{v_{w}}{2 \Delta L}\right) \end{array} \] \( 20.5 \) points Which of these expressions correctly represents the condition for the desired interference at location-A? \[ \Delta L=\left(n+\frac{1}{2}\right) \lambda \] \[ \begin{array}{l} \Delta L=\frac{\lambda}{n} \\ \Delta L=\frac{n}{2}+\lambda \\ \Delta L=\left(n+\frac{\lambda}{2}\right) \end{array} \] The above condition for the desired interference at location A can be written in terms of the frequency: \[ \begin{array}{l} f=\frac{n}{2}+\frac{v_{w}}{\Delta L} \\ f=\left(n+\frac{1}{2}\right) \frac{\Delta L}{v_{w}} \\ f=\left(n+\frac{1}{2}\right) \frac{v_{w}}{\Delta L} \\ f=\left(n+\frac{v_{w}}{2 \Delta L}\right) \\ f=n \frac{v_{w}}{\Delta L} \end{array} \] \( 0.5 \) points Suppose that the distance indicated \( d \) in the figure is \( 6.5 \mathrm{~mm} \), what is the difference in path lengths between the waves traveling from the two sources to location-A? (report your answer in mm) \( 0.5 \) points Taking \( d \) to be the same as above, what is the difference in path lengths between the waves traveling from the two sources to location-B? (report your answer in \( \mathrm{mm} \) ) Type your answer... \( 0.5 \) points The speed of ultrasonic waves in human tissue depends on the kind of tissue and other conditions. Since the researcher did not communicate a specific speed to consider in your calculations, you perform a quick search to help you make a reasonable assumption. Below are some resources that turned up in a quick search. Based on these resources (or your own research) pick a reasonalife value for the speed of ultrasound in human tissue to use in the rest of your calculations. Report that speed in \( \mathrm{m} / \mathrm{s} \) in the box below. Resources - [link to a manuscript on the NIH server], - [Physiopedia], - [Abstract for a chapter in a book on Ultrasound Energy], -... \( 0.5 \) points Using the conditions identified above, as well as the assumed value for the speed, pick an integer \( n \) such that the resulting frequency is in the range \( 1 \mathrm{MHz} \) to \( 2 \mathrm{MHz} \). Report your choice of \( \mathrm{n} \), and the estimated frequency. Be careful with the units.