Home /
Expert Answers /
Advanced Math /
it-is-given-that-alpha-is-in-f-why-does-this-imply-that-z-p-alpha-is-a-subset-of-f-2-what-does-i-pa988
(Solved): It is given that alpha is in F. Why does this imply that Z_p(alpha) is a subset of F?2. What does i ...
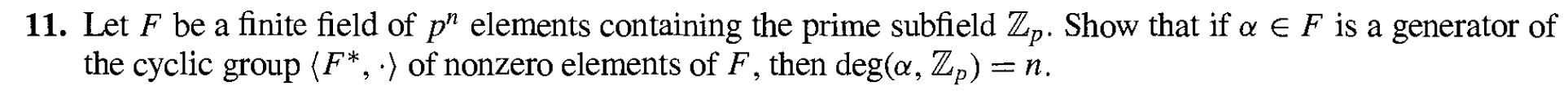
- It is given that alpha is in F. Why does this imply that Z_p(alpha) is a subset of F?
2. What does it mean that “alpha is a generator of the multiplicative cyclic group F* of nonzero elements of F”? How does this show that Z_p(alpha)=F?
3. What is meant by |F|=p^n and how does this show that the degree of alpha over Z_p is n?
11. Let be a finite field of elements containing the prime subfield . Show that if is a generator of the cyclic group of nonzero elements of , then .
Expert Answer
In this context, the field F is defined to contain the prime subfield which consists of the eleme...