(Solved): Let \( f(t) \) be a function (scalor). Write \( f(t) \) as a vector function \( r(t) \). (1) \( f(x ...

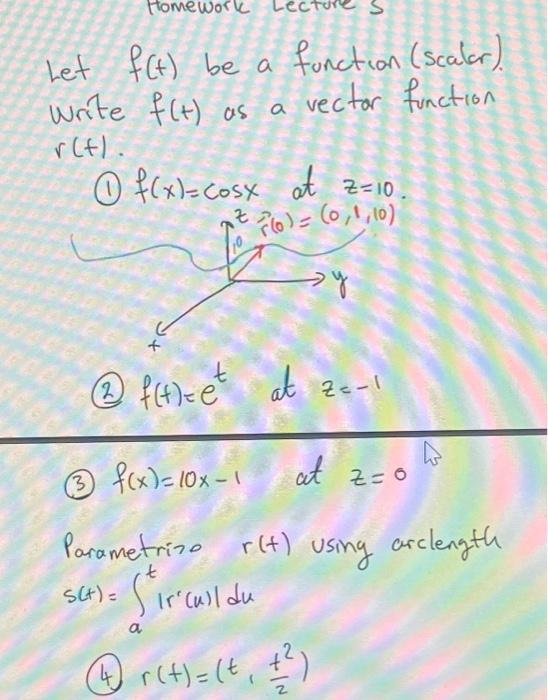
Let \( f(t) \) be a function (scalor). Write \( f(t) \) as a vector function \( r(t) \). (1) \( f(x)=\cos x \) at \( z=10 \). (2) \( f(t)=e^{t} \) at \( z=-1 \) (3) \( f(x)=10 x-1 \) at \( z=0 \) Parametrine \( r(t) \) using arclength \( s(t)=\int_{a}^{t}\left|r^{\prime}(u)\right| d u \) (4) \( r(t)=\left(t, \frac{t^{2}}{2}\right) \)