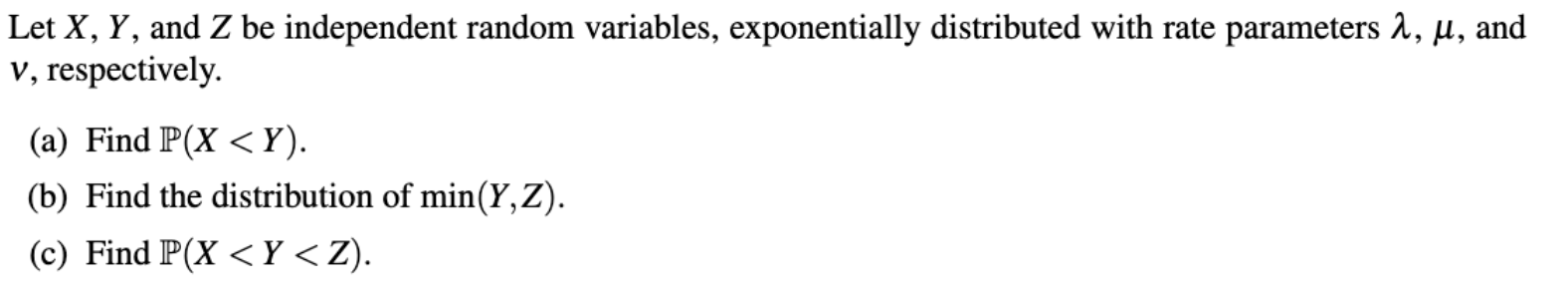Home /
Expert Answers /
Statistics and Probability /
let-x-be-a-poisson-distributed-random-variable-with-parameter-1-show-that-p-x-gt-t-lt-e-t-pa384
(Solved): Let x be a Poisson distributed random variable with parameter 1 . Show that P(x>=t)<=(e^(t- ...
Let
xbe a Poisson distributed random variable with parameter 1 . Show that
P(x>=t)<=(e^(t-1))/(t^(t))for
t>=1. Hint: You might want to first show that
P(x>=t)<=e^(-\theta t)e^(e^(\theta )-1)for
\theta >=0. Remark: This bound can be used to show the following threshold phenomena: Let
M_(n)be the maximum of
ni.i.d. Poisson distributed random variables of parameter 1 . For any fixed
ainR, as
n->\infty , we have that
P(M_(n)>=(1+a)log(n)/(loglogn))->{(1 if a<0),(0 if a>0):}Let
x,Y, and
Zbe independent random variables, exponentially distributed with rate parameters
\lambda ,\mu , and
u , respectively. (a) Find
min(Y,Z)