(Solved): Long-Term Behaviors of Matrix Models 1. (3 points) A matrix \( M \) models a linear discrete-time s ...

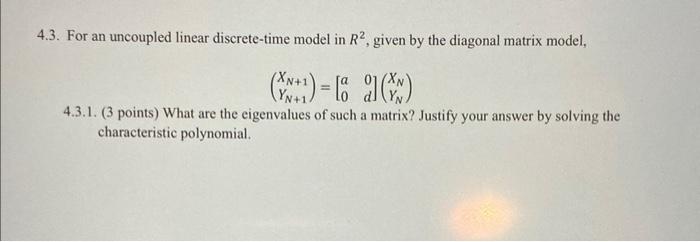
Long-Term Behaviors of Matrix Models 1. (3 points) A matrix \( M \) models a linear discrete-time system. If \( \left(\begin{array}{l}X_{0} \\ Y_{0}\end{array}\right) \) is the initial vector, one can simulate the model by applying the matrix \( N \) times to the initial vector as follows: \[ \left(\begin{array}{l} X_{N} \\ Y_{N} \end{array}\right)=M^{N}\left(\begin{array}{l} X_{0} \\ Y_{0} \end{array}\right) \] where, \( N=0,1,2, \ldots \) is the discrete time steps. You learned in LS30B that you can obtain similar results using diagonalization and coordinate transform as given below: \[ \left(\begin{array}{l} X_{N} \\ Y_{N} \end{array}\right)=T D^{N} T^{-1}\left(\begin{array}{l} X_{0} \\ Y_{0} \end{array}\right) \ldots(\text { Equation I }) \] Explain the meaning of Equation I using words, relevant notations, and diagrams. Make sure to describe what are \( T, T^{-1} \) and \( D \) stand for. 4.2. (3 points) Given \( M=\left[\begin{array}{ll}4 & 2 \\ 5 & 1\end{array}\right] \), find the \( D \) matrix. 3. For an uncoupled linear discrete-time model in \( R^{2} \), given by the diagonal matrix model, \[ \left(\begin{array}{l} X_{N+1} \\ Y_{N+1} \end{array}\right)=\left[\begin{array}{ll} a & 0 \\ 0 & d \end{array}\right]\left(\begin{array}{l} X_{N} \\ Y_{N} \end{array}\right) \] 4.3.1. (3 points) What are the eigenvalues of such a matrix? Justify your answer by solving the characteristic polynomial. 4.3.2. (4 points) Given initial condition, \( \left(\begin{array}{l}15 \\ 30\end{array}\right) \) compute \( \left(\begin{array}{l}X_{15} \\ Y_{15}\end{array}\right) \). Show steps as needed.