(Solved): MATLAB ASSIGNMENT PART 3:Thank you! This exercise will use MATLAB to verify the rank theorem for mat ...

This exercise will use MATLAB to verify the rank theorem for matrices $A1,A2$, and $A3$ from Exercise 2. A. Find bases for the null space, column space, and row space of matrix A1 - null (A1, ' $r$ ') -- each column represents a vector in a basis for Nul A1 - Recall the process of finding the column space of $A??$ When $[B$, pivcol] $=$ rref (A1) is used, write a single command* to find a basis for the column space of A1 so that each column represents a vector in a basis for Col A1. (DO NOT use the command colspace) - Now, think about how we find a basis for the row space. Write a single command* to find a basis for the row space of A1 so that each row represents a vector in a basis for Row A1. Exercise 3 - The Rank Theorem $3\mathrm{A}$ A1 \% display A1 first $N1=$ null(A1, ' $r^{?})\%$ each column represents a vector in a basis for Nul A1 $[B$, pivcol] = rref(A1) $\%$ write a single command for column space of A1 so that each column represents a vector in a basis for Col A1 $C1=$ $\%$ write a single command for row space of A1so that each row represents a vector in a basis for Row A1 R1 $=$ A1 \% display A1 first $\mathrm{N}1=$ null (A1, ' $r$ ') \% each column represents a vector in a basis for Nul A1 $[B$, pivcol] $=\mathrm{rref}(A1)$ \% write a single command for column space of A1 so that each column represents a vector in a basis for col A1 $\mathrm{Cl}=$ \% write a single command for row space of A1so that each row represents a vector in a basis for Row A1 $R1=$ 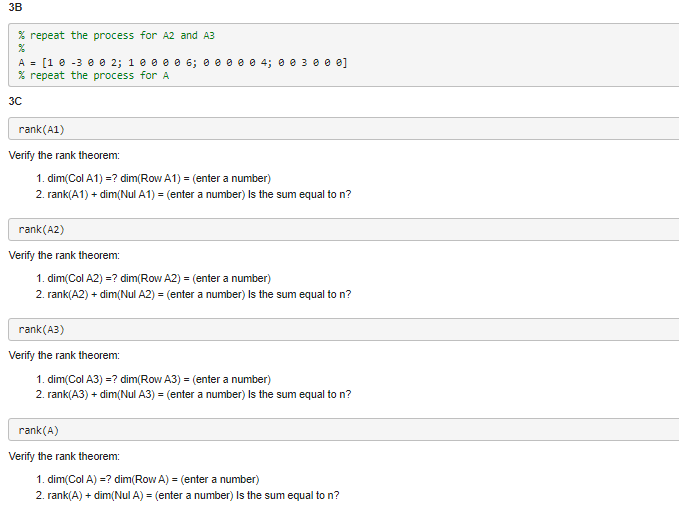3B \% repeat the process for $A2$ and $A3$ $\%$ $\%$ repeat the process for $A$ $3\mathrm{C}$ $\mathrm{rank}(A1)$ Verify the rank theorem: 1. $\dim (\mathrm{Col}A1)=$ ? $\dim ($ Row $A1)=($ enter a number $)$ 2. $\mathrm{rank}(\mathrm{A}1)+\dim (\mathrm{Nul}\mathrm{A}1)=($ enter a number $)$ ls the sum equal to $\mathrm{n}$ ? $\mathrm{rank}(A2)$ Verify the rank theorem: 1. $\dim (\mathrm{Col}A2)=$ ? $\dim (\mathrm{Row}A2)=($ enter a number) 2. $\mathrm{rank}(A2)+\dim ($ Nul $A2)=($ enter a number $)$ ls the sum equal to $n$ ? $\mathrm{rank}(A3)$ Verify the rank theorem: 1. $\dim (\mathrm{Col}A3)=$ ? $\dim (\mathrm{Row}A3)=($ enter a number $)$ 2. $\mathrm{rank}(A3)+\dim ($ Nul $A3)=($ enter a number $)$ ls the sum equal to $n$ ? $\mathrm{rank}(A)$ Verify the rank theorem: 1. $\dim (\mathrm{Col}A)=$ ? $\dim ($ Row $A)=($ enter a number $)$ 2. $\mathrm{rank}(A)+\dim (\mathrm{Nul}A)=($ enter a number $)$ is the sum equal to $n$ ? B. Repeat the process to - find bases for the null space, column space, and row space of matrices $\mathrm{A}2$ and $\mathrm{A}3$ - find bases for the null space, column space, and row space of matrix A (see matrix A in the template file) and verify if your code for finding the bases for the column space and row space is correct C. For each matrix (A1, A2, A3, and A), find the rank (use the command rank) and verify the rank theorem in your report. ${}^{?}$ The command for Col A and Row A must work for all matrices A.